Thursday, May 6, 2010

How To Find Out What Makes Your Customers Buy More Using the Chi-Square Independence Test in Excel

Chi-Square Independence

Test in Excel

For Marketing



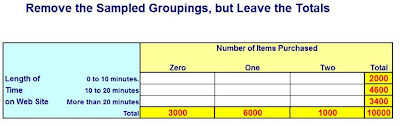
If there was one question that every single marketing manager and business owner would like an answer to, it might be this one: “What makes my customers buy more???” Anyone who has had that question on their mind will like this article. If you have been collecting data on your customers, you can use Excel to perform a statistical procedure called the Chi-Square Independence Test to find out what factors seem to have made a difference when your customers make larger purchases.

The attached video demonstrates how to perform the Chi-Square Independence Test in Excel to determine whether the size of a customer’s online order is related to the amount of time that the customer has spent on the web site. The video walk you through step-by-step in Excel how to perform the test and interpret the output:


Here is a Step-By-Step Video Showing Exactly How To Find Out What Makes Your Customers Buy More With the Chi-Square Independence Test in Excel:
(Is Your Sound Turned On?)



What Is the Chi-Square Independence Test?

The Chi-Square Independence Test can be quickly summed up as follows: This test determines whether two attributes of one object are related (not independent of each other). The object in mind is your customer. One of your customer’s attributes that we will evaluate is order size. The other attribute can be anything connected with individual orders that you consistently collect data on and that you would like to know whether order size is related to.

One caveat should be mentioned up front about this test. The Chi-Square Independence Test only shows if two attributes of an object are related. It does not prove causality. However, where’s there’s smoke, there’s fire. Even if one attribute that you are testing (in this case, customer’s time on your web site) does not directly cause the other (order size), there must be something related to time on the web site that does cause increased order size. This test will definitely point you in the right direction in determining what the most important factors are that cause larger orders.




Here's How We Did Our Chi-Square Independence Test

Here’s how we did the test that you’ll see in the video. First we took a random sample of 10,000 visitors to a commercial website from a much larger universe of visitors to that site in the same time period. We collected data on each of those customers. The data we collected for each customer was 1) how items that customer purchased and 2) how long that customer stayed on the web site during the visit that they ordered.

We will then use the Chi-Square Independence Test to determine within 99% certainty whether the customer’s order size is related to (not independent of) time spent on the web site. In this test we are making a few assumptions that are probably incorrect, but will be made in order to keep everything simple for demonstration purposes. We will assume that each visitor visited the site only once and that no other factors that could have influenced order size were varied during the test.


The 3 Overall Steps in the Chi-Square Independence Test

There are 3 overall steps in the Chi-Square Independence Test. They will be explained in greater detail below and are also shown in the video. These overall steps are:

1) Arrange the sampled data in a Contingency Table.

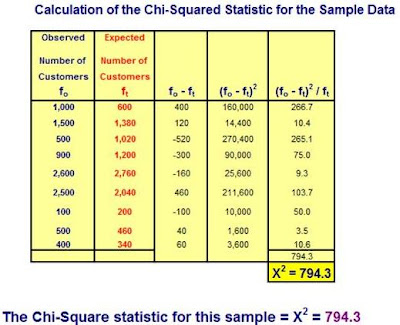
2) Calculate the Chi-Square Statistic for the Sampled Data.

3) Compare the above Chi-Square Statistic with the Critical Chi-Square Statistic. If the Chi-Square Statistic is greater than the Critical Chi-Square Statistic, we can state that the two attributes of the object are related (are not independent).



Step1) Arrange the Sampled Data in a Contingency Table

The first step after data sampling is to arrange the data on a Contingency Table. The video shows exactly how this is done. In the Contingency Table, all of the 10,000 site visitors sampled are placed into 1 of 9 groups of similar visitors. The Contingency Table has visitor data divided up into 3 columns based on number of items a customer purchased (0, 1, or 2) and into 3 rows based on the time that the customer spent on the web site (0 to 10 minutes, 10 to 20 minutes, and more than 20 minutes). Each of the 10,000 randomly-sampled site visitors will be placed into 1 of the 9 possible groups on this 3 x 3 Contingency Table. Once again, watch the video to get a clear picture of this.

chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View

The next part of Step 1) is to create a duplicate Contingency Table which will contain the number of visitors in each of the 9 groups that would have been expected based upon the totals for each row and column on the original Contingency Table. The expected number of visitors in each group is calculated from the following formula: (Total number of visitors in a row) x (Total number of visitors in a column) / (Total overall number of visitors). Watching the video will probably make that calculate easier to visualize.
chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View

chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View




Here are both the Actual and Expected Contingency Tables:
chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View




Step 2) Calculate the Chi-Square Statistic for the Sampled Data
We can now calculate the Chi-Square Statistic for the sampled data and also the Critical Chi-Square Statistic. Both of these values will be compared to determine whether the two attributes are related or not.

Watching the video is the easiest way to comprehend how to calculate the Chi-Square Statistic for the sampled data. Briefly, here is how the calculation is performed. There are two Contingency Tables. The first Contingency Table is a 3 x 3 matrix containing actual data from the customer survey. The 2nd Contingency Table is also a 3 x 3 matrix containing the expected number of customers in each group (each of the 9 cells of the matrix holds the data for each of the 9 visitor groupings).

We will label data from the 9 cells of the original Contingency Table as f0i (that is, f01, f02, f03,…, f09). We will label data from each of the 9 cells of the Expected Value Contingency Matrix as fti (that is, ft1, ft2, ft3,…, ft9).

The Chi-Square Statistic for the sampled data can now be calculated from the following formulas:

chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View


Chi-Square Statistic = Sum of (f0i - fti ) / fti as i goes from 1 to 9. Once again, the video provide a clear picture of this calculation. The Chi-Square Statistic for the sampled data in the test we are performing equals 794.3.



Now we need to calculate the Critical Chi-Square Value. The Chi-Square Critical Value is determined by 2 things: 1) the Degrees Of Freedom inherent to the Contingency Table and 2) the required degree of certainty.

The Degrees of Freedom inherent to any Contingency Table is calculated by the following formula:

DOF = (r – 1) x (c – 1) where r = number of rows in the table and c = number of columns in the table. In a 3 x 3 Contingency table, there are 3 rows and 3 columns. In this case, DOF = (3 – 1) x (3 – 1) = 4

We require a 99% Degree of Certainty. Alpha is therefore equal to 0.01.

Alpha = 1 – Required Degree of Certainty = 1 – 0.99 = 0.01

We calculate the Critical Chi-Square Value by plugging the Degree of Freedom and the Alpha into the following Excel formula:

CHIINV(DOF,Alpha) = CHIINV(4,0.01) = 13.28
chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View



We now have:

Chi-Square Statistic for the Sample Data = 794.3

Critical Chi-Square Value = 13.28



Step 3) Compare the above Chi-Square Statistic with the Critical Chi-Square Statistic

chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel
Click On Image To See Enlarged View


Compare the Chi-Square Statistic (794.3) with the Critical Chi-Square Value (13.28).

Since the Chi-Square Statistic is greater than the Critical Chi-Square Value, we can state with 99% certainty that the two attributes, order size and time on web site, are related. It would not be correct to state the time on site causes larger orders (although it might), but the two are definitely related. If time on site does not directly cause larger orders, time on site is probably closely related to something that does cause the larger orders.chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel

Please post any comments you have on this article. Your opinion is highly valued!




If You Like This, Then Share It...
chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel chi squared, chi square, chi squared test, chi squared table, chi squared distribution, chi squared distribution, independent test, independence test, statistical analysis in excel

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at
Labels: , , , ,

2 comments:

Subscribe to: Post Comments (Atom)