Overview of Binomial Distribution in Excel 2010 and Excel 2013

This is one of the following four articles on the Binomial Distribution in Excel

Overview of the Binomial Distribution in Excel 2010 and Excel 2013

Solving Problems With the Binomial Distribution in Excel 2010 and Excel 2013

Normal Approximation of the Binomial Distribution in Excel 2010 and Excel 2013

Distributions Related to the Binomial Distribution

 

Overview of the Binomial

Distribution

The binomial distribution is the discrete probability distribution of the number of successes in n successive independent binary trials. Each trial has the same probability p of a successful outcome of the binary trial’s two possible outcomes.

p = probability of success in each and every binary trial

n = the total number of binary trials

k = a specific number of successful outcomes of n binary trials

X = the actual number of successful outcomes of n binary trials

The probability that X (the actual number of successful outcomes of n successive, independent binary trials each having probability p of a successful outcome) equals a specific k is given as follows:

(Click On Image To See a Larger Version)

for k = 0, 1, 2, …, n,

where

 (Click On Image To See a Larger Version)

is sometimes referred to as “n choose k.” This is called the binomial coefficient and the source of the name of the binomial distribution. The binomial coefficient is equal to the number ways that k items can be combined to create n elements. This is the number combinations that k items can be arranged to create n total elements.

A different ordering of the same k items does not create a new combination. For example, the three elements A, B, and C can only be arranged into one combination of three total elements. ABC is not a different combination than CAB is. A different ordering of the same three elements does, however, create a new permutation.

The Excel formula for the total possible number of combinations of k elements into n total elements is given by the following:

 (Click On Image To See a Larger Version)

COMBIN(n,k) is the Excel combination formula.

A combination should be differentiated from a permutation. The number of possible combinations is the total number of ways that k elements can be arranged into n total elements when order does not matter. The number of possible permutations is the total number of ways that k elements can be arranged into n total elements when order does matter.

There are always more permutations of k objects than combinations because, for example, ABC and CAB are two different permutations of the letters A, B, and C but not two different combinations of those three letters. Re-arrangement of the same elements within a set creates a new permutation but does not create a new combination.

The Excel formula for the total possible number of permutations of k elements into n total elements is given by the following:

 (Click On Image To See a Larger Version)

PERMUT(n,k) is the Excel permutation formula.

Note that the following is true:

(Click On Image To See a Larger Version)

 

Each Trial is a Bernoulli Trial

Each individual trial is called a Bernoulli trial. The outcome of a Bernoulli trial can be described by the binomial distribution with n = 1. A Bernoulli trial follows the Bernoulli distribution, which is a special case of the binomial distribution where n = 1.

 

Maximum Sample Size Rule

The binomial distribution should not be applied to a single random sample taken from a population unless the population is at least 10 times larger than the sample size.

 

Binomial Distribution Has Two Parameters n and p

A binomial distribution is fully described by two parameters n (the total number of trials) and p (the constant and unchanging probability of success on each trial). The binomial distribution is denoted as follows:

B(n,p)

The binomial distribution is a discrete distribution because its probability equation Pr(X = k) is calculated only for values of k, which can only assume integer values.

The binomial distribution describes the distribution of the number of successes, X, if the following four conditions exists:

1) Each trial is a single Bernoulli trial, which is a binary event having only one of two outcomes: success or failure.

2) The total number of trials = n.

3) Each trial is independent of all other trials.

4) The probability of success in each trial is p, which is constant in all trials. The probability of failure = q = 1 – p.

The binomial distribution requires that each sample taken is returned to the population before the next sample is taken. Samples are always taken from the same population. This is called sampling with replacement.

If samples taken are not returned to the population, the hypergeometric distribution is used in place of the binomial distribution. This is called sampling without replacement. If sample size is much smaller than the population from the sample was drawn, the binomial distribution provides a good approximation of the hypergeometric distribution when sampling without replacement is performed. The population size should be at least ten times as large of the sample size for this substitution to be valid.

 

Population Parameters of the Binomial Distribution

n = number of trial

p = probability of success on each trial

q = 1 – p = probability of failure on each trial

If X ~ B(n,p) (X is a binomially-distributed variable having n trials and the probability p of success on each trial. X is a variable representing the number of successes given n and p), then the following is true:

Expected Value(X) = Mean(X) = μ_X = np

Variance(X) = σ²_X = npq

Standard Deviation(X) = σ_X =

Applying these formulas to a basic example illustrates the intuitive nature of these formulas. If a coin were flipped 12 times (n = 12) and the coin was fair (p = 0.5 and q = 1 – p = 0.5), then the following are true regarding X, the number of successes (heads) in n trials (coin flips) given the probability p of success (heads) on each trial (coin flip):

Expected Value(X) = Mean(X) = μ_X = 12 * 0.5 = 6

Variance(X) = σ²_X = npq = 12 * 0.5 * 0.5 = 3

This makes sense because 6 heads is the number of heads that one would expect to occur with 12 flips of a fair coin.

 

Binomial Distribution’s PDF and CDF

PDF = Probability Density Function

CDF = Cumulative Distribution Function

 

Binomial Distribution’s PDF - Probability Density Function

The binomial distribution’s PDF is given by the following:

 (Click On Image To See a Larger Version)

for k = 0, 1, 2, …, n, where

(Click On Image To See a Larger Version)

f(k;n,p) = Pr(X = k) is the probability that X, the number of successes, equals k for n independent, successive Bernoulli trials each having the probability p of success.

For example, for the following parameters:

k = 4

n = 10

p = 0.5

Each unique binomial distribution is fully described by two parameters n and p. This binomial distribution is the distribution X successes in n = 10 trials with p = 0.5 probability of a successful outcome in each and every one of the 10 trials.

This binomial distribution’s PDF calculates that the probability that X (the actual number of successful outcomes) equal k which is 4.

The Excel formula to calculate the binomial distribution’s PDF is the following:

f(k;n,p) = Pr(X = k) = BINOM.DIST(k, n, p , FALSE)

FALSE indicates that this Excel formula is calculating the binomial distribution’s PDF and not the CDF for this k, n, and p. “False” answers the question of the calculation is cumulative (which is the case if calculating the CDF – Cumulative Distribution Function) on not cumulative (which is the case if calculating the PDF – Probability Density Function).

Excel 2010 and later also use the formula BINOM.DIST() which is equivalent to BINOMDIST() that is used by earlier versions of Excel. It should be noted that many of the equivalent but upgraded formulas in Excel 2010 are more accurate than the original versions and should be used when possible. Microsoft recommends using the latest possible versions of any statistical formulas.

BINOM.DIST(4,10,0.5,FALSE) = 0.2051

This Excel binomial PDF calculation indicates that there is a 20.51 percent chance of exactly 4 successes in 10 independent, successive Bernoulli trials with 50 percent probability of success on each trial.

A graph of the binomial distribution’s PDF for this unique binomial distribution (n= 10 and p = 0.5) shows the probability that X = 4 is 0.2051.

 (Click On Image To See a Larger Version)

The binomial distribution’s curve shifts from left to right as p increases. This is shown is the following graphs of the binomial’s PDF for n = 10 when p = 0.2 and then as p = 0.8. Note that the graphs of p = 1/5 (0.2) and p = 4/5 (0.8) are mirror images of each other about the mean of 5.

 (Click On Image To See a Larger Version)

 (Click On Image To See a Larger Version)

 

Binomial Distribution’s CDF - Cumulative Distribution Function

The binomial distribution’s CDF is as follows:

F(k;n,p) = Pr(X ≤ k). This is the probability that X, the number of successes in n Bernoulli trials each having the probability p of a successful outcome, equals up to k.

The binomial distribution’s CDF is given by the following:

 (Click On Image To See a Larger Version)

is the “floor” under k, i.e., the greatest integer less than or equal to k.

The Excel formula to calculate the binomial distribution’s CDF is the following:

F(k;n,p) = Pr(X ≤ k) = BINOM.DIST(k, n, p , TRUE)

TRUE indicates that this Excel formula is calculating the binomial distribution’s CDF and not the PDF for this k, n, and p.

BINOM.DIST(4,10,0.5, TRUE) = 0.3769

There is a 37.69 percent chance of up to 4 successes in 10 independent, successive Bernoulli trials with 50 percent probability of success on each trial. A graph of the binomial distribution’s CDF for this unique binomial distribution (n= 10 and p = 0.5) shows the probability that X = 4 is 0.3769.

 (Click On Image To See a Larger Version)

The CDF for any distribution always varies from a minimum value of 0 on the left to a maximum value of 1 on the right. Just as with the PDF, the binomial distribution’s CDF shifts from left to right as p increases. This is shown is the following graphs of the binomial’s CDF for n = 10 when p = 0.2 and then as p = 0.8.

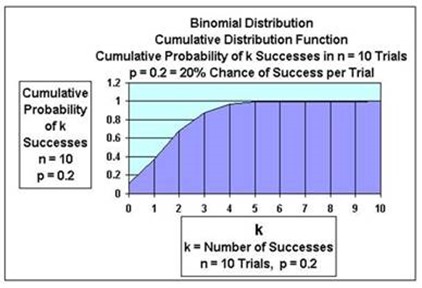
 (Click On Image To See a Larger Version)

 (Click On Image To See a Larger Version)

 

Excel Master Series Blog Directory

 

Click Here To See a List Of All

Statistical Topics And Articles In

This Blog

 

You Will Become an Excel Statistical Master!