Single-Factor ANCOVA in 8 Steps in Excel

Single-Factor ANCOVA

in Excel in 8 Steps

Overview

Just like single-factor ANOVA, ANCOVA is used to determine if there is a real difference between the means of two or more sample groups of continuous data. Like ANOVA, ANCOVA answers the following question: Is it likely that all sample groups came from the same population? Unlike ANOVA, ANCOVA allows the researcher to remove the affects of an outside, unrelated factor or variable that might cause ANOVA to produce an incorrect result.

Suppose that a group of boys were the subjects of an ANOVA test to determine if the factor of height had an effect on size of a boy’s vocabulary. ANOVA would very likely indicate that the factor of height has a significant affect on the size of a boy’s vocabulary. This is particularly true if the boys are sampled over a wide range of ages. Older boys will generally be taller and have a larger vocabulary than younger boys. The causal factor for increased vocabulary would intuitively be age, not height. If all boys were sampled from the same age group, then height should not be a factor in the size of a boy’s vocabulary. The natural corollary to this statement is that removing the effects of age would allow a researcher to much more accurately determine if height has a significant effect on vocabulary size.

That is exactly what ANCOVA does. ANCOVA is used in place of single-factor ANOVA if a third “confounding” variable is suspected of affecting the measured values of the data points in each of the ANOVA groups. Single-factor ANOVA is considered to have two variables; the independent variable is a categorical variable that separates data points into different groups and the dependent variable is the continuous scale that is used to measure the data values. ANCOVA removes that affect of a third “confounding” variable on the measured data values of the Dependent variable.

ANCOVA = Analysis of Covariance

ANCOVA, Analysis of Covariance, can be used in place of single-factor ANOVA to remove the effects of an outside factor that might be confounding the results of the ANOVA test. The outside factor is a third variable is called a "Covariate," a “Covariate Variable,” a “confounding variable,” or a “nuisance variable.” ANCOVA is essentially a single-factor ANOVA performed after the variance attributed to the third variable has been statistically removed.

Single-factor ANOVA analyzes sample groupings of objects that described by two variables. The variable that designates the group into which the object is assigned is a categorical variable and is referred to in ANOVA as the independent variable. Single-factor ANOVA is used to determine whether the factor described by the variable has a significant effect on data values, specifically whether samples grouped according to different levels of the factor (different values of the categorical variable) have significantly different means.

The other variable of single-factor ANOVA is the continuous variable used as the measurement scale for all data points in the sample groups. This variable is known as the dependent variable.

If an additional factor is known to affect these measured values of the data points, this factor is designated as the third variable and is the Covariate variable. The Covariate Variable must be a continuous variable and must have a known value for each sample data point. ANCOVA performs the same function and calculations of single-factor ANOVA after removing the variance attributed to the Covariate factor or variable.

Null and Alternative Hypotheses for ANCOVA

The Null Hypothesis for ANCOVA is exactly like that of single-factor ANOVA and states that the sample groups ALL come from the same population. This would be written as follows:

Null Hypothesis = H₀: µ₁ = µ₂ = … = µ_k (k equals the number of sample groups)

Note that Null Hypothesis is not referring to the sample means, s₁ , s₂ , … , s_k, but to the population means, µ₁ , µ₂ , … , µ_k.

The Alternative Hypothesis for ANCOVA states that at least one sample group is likely to have come from a different population. Like single-Factor ANOVA, ANCOVA does not clarify which groups are different or how large any of the differences between the groups are. This Alternative Hypothesis only states whether at least one sample group is likely to have come from a different population.

Alternative Hypothesis = H₀: µ_i ? µ_j for some i and j

ANCOVA Example in Excel

A company is attempting to determine if either of two sales-training methods produces a significantly better increase in a salesperson’s monthly sales. The company simultaneously sent one group of ten salespeople through one of the training programs and sent another group of ten salespeople through the other training program. The change in average monthly sales for each salesperson after completion of the program was recorded.

A single-factor ANOVA of the sales increases for each of the two groups did not evidence any significant different between the effectiveness of the two training programs in producing sales increases. This will be shown within the example.

A senior manager of the company noticed that the salespeople who had more years of experience seemed to have had higher sales increases after the training as a whole than salespeople with less experience. The senior manager speculated that a salesperson’s amount of experience had a direct effect on that salesperson’s ability to benefit from additional training program.

The senior manager wanted to analyze the post-training sales results to determine if one training program significantly outperformed the other but also wanted to remove the effects of the amount of previous experience which might make a difference the salespeople’s ability to implement the training and increase sales.

ANCOVA is the correct statistical tool for this task. This example will demonstrate ANCOVA detecting a difference in sample groups that single-factor ANOVA could not.

Below is the sample data:

 
(Click On Image To See a Larger Version)

Each of the subjects who underwent the training can be described by the following three variables used in ANCOVA:

Independent Variable – This is the categorical variable of Training Method type. The overall objective of the ANCOVA is to determine if levels of the factor of training program type produced significantly different sales increases.

Dependent Variable – This continuous variable is the monthly sales increase for each salesperson who underwent either of the two training programs. Note that values of this variable are colored black.

Covariate Variable – This continuous variable is the number of years of prior experience that each salesperson had prior to undergoing the training for either of the two programs. It is speculated that this variable might have significantly affected the salespeople’s abilities to implement the training program and increase sales. One of the objectives of this ANCOVA is to remove effects of this variable so that the results will more accurately determine whether one training program is more effective than the other. Note that values of this variable are colored red.

ANCOVA can be performed in Excel in 8 steps. Before performing these steps, ANCOVA’s required assumptions will be listed below as follows:

ANCOVA’s Required Assumptions

ANCOVA Has the Following Same Required Assumptions as Single-Factor ANOVA

Like single-factor ANOVA, ANCOVA has the following six required assumptions whose validity should be confirmed before this test is applied. The six required assumptions are the following:

1) Independence of Sample Group Data Sample groups must be differentiated in such a way that there can be no cross-over of data between sample groups. No data observation in any sample group could have been legitimately placed in another sample group. No data observation affects the value of another data observation in the same group or in a different group. This is verified by an examination of the test procedure.

2) Sample Data Are Continuous Sample group data (the dependent variable’s measured value) can be ratio or interval data, which are the two major types of continuous data. Sample group data cannot be nominal or ordinal data, which are the two major types of categorical data.

3) Independent Variable is Categorical The determinant of which group each data observation belongs to is a categorical, independent variable. ANCOVA uses a single categorical variable that has at least two levels. All data observations associated with each variable level represent a unique data group and will occupy a separate column on the Excel worksheet.

4) Extreme Outliers Removed If Necessary ANCOVA is a parametric test that relies upon calculation of the means of sample groups. Extreme outliers can skew the calculation of the mean. Outliers should be identified and evaluated for removal in all sample groups. Occasional outliers are to be expected in normally-distributed data but all outliers should be evaluated to determine whether their inclusion will produce a less representative result of the overall data than their exclusion.

5) Normally-Distributed Data In All Sample Groups ANCOVA is a parametric test having the required assumption the dependent-variable data from each sample group come from a normally-distributed population. Each sample group’s dependent-variable data should be tested for normality. Normality testing becomes significantly less powerful (accurate) when a group’s size fall below 20. An effort should be made to obtain group sizes that exceed 20 to ensure that normality tests will provide accurate results. Like single-factor ANOVA, ANCOVA is relatively robust to minor deviation from sample group normality. There are a number of different ways of testing sample groups for normality. The simplest way is to create a histogram of the data in each sample group. Each histogram should be bell-shaped, which would indicate that more points in each data sample were close to the sample's mean than away from it. A normal probability plot for each sample group could also be constructed. A number of other normality hypothesis tests can also be applied to each data sample to determine whether to reject each test's Null Hypothesis that the sample group is normally distributed. The more well-known of these tests include the Kolmogorov-Smirnov test, the Anderson-Darling test, and  the Shapiro-Wilk test. The Shapiro-Wilk test is considered the most powerful of those three is applied most often. The following link leads to step-by-step instructions in this blog on how to perform the Shapiro-Wilk test in Excel on data samples for single-factor ANOVA: http://blog.excelmasterseries.com/2014/05/shapiro-wilk-normality-test-in-excel_29.html

6) Relatively Similar Variances In All Sample Groups ANCOVA requires that sample groups are obtained from populations that have similar variances. This requirement is often worded to state that the populations must have equal variances. The variances do not have to be exactly equal but do have to be similar enough so the variance testing of the sample groups will not detect significant differences. The variances of sample groups are considered similar if no sample group variance is more than twice as large as the variance of another sample group. Variance testing becomes significantly less powerful (accurate) when a group’s size fall below 20. An effort should be made to obtain group sizes that exceed 20 to ensure that variance tests will provide accurate results. Two common hypothesis tests used to determine whether sample variances are similar are Levene's test and the Brown-Forsythe test. Here is a link leading to another article in this blog showing exactly how to perform both tests in Excel on sample groups for single-factor ANOVA:   http://blog.excelmasterseries.com/2014/05/levenes-and-brown-forsythe-tests-in_29.html

ANCOVA Has the Following Additional Required Assumptions

7) Covariate Data Are Continuous Covariate values at each data point can be ratio or interval data, which are the two major types of continuous data.

8) Covariate Data Have a Linear Relationship With Dependent Variable Data This can be quickly observed by creating a scatterplot of Covariate/Dependent data points. Linearity or nonlinearity between the two variables will be quickly observable on the scatterplot.

9) The Least-Squares Lines For Covariate/Dependent Variable Data Have Similar Slopes For Each Sample Group Once again this can be quickly observed on a scatterplot of Covariate/Dependent data points. A least-squares line for data points from one sample group (one of the training methods) can be compared with the least-square line for data points of the other sample group. Least-squares lines for data from different sample groups should have similar slopes. This ensures that the categorical variable (the training method used in this case) did not have an effect on the relationship between the Covariate and Dependent data.

The overall purpose of this chapter is to demonstrate the differences between performing single-factor ANOVA and performing ANCOVA. For this reason we will forego validation of the above required assumptions. This section of this manual covering Single-Factor ANOVA provides detailed discussion on how to perform normality and variance testing of ANOVA sample groups. These same methods can be directly applied to ANCOVA sample groups for the dependent variable.

A scatterplot of Covariate/Dependent data pairs can be quickly created in Excel to validate assumptions 8 and 9.

(Click On Image To See a Larger Version)

(Click On Image To See a Larger Version)

The slopes of both least squares lines are similar enough to verify that the categorical variable (the type of training method) does not affect the relationship between the Covariate Variable (X – Prior Years of Experience) and the Dependent Variable (Y – Monthly Sales Increase)

When the required assumptions of ANCOVA have been validated, ANCOVA can be performed in Excel as follows:

ANCOVA in Excel - The 8 Steps

 

Step 1) Run Single-Factor ANOVA on the Dependent Variable Data

Run Excel Single-Factor ANOVA on the Y (dependent variable) data in order to obtain SS_total(Y), SS_within(Y), and SS_between(Y)

 

Step 2) Run Single-Factor ANOVA on the Covariate Variable Data

Run Excel Single-Factor ANOVA on the X (covariate) data in order to obtain SS_total(X) and SS_within(X)

 

Step 3) Calculate r_total²

Calculate r_total² for Y_total. r_total² is derived from r_total, which is the overall correlation between X and Y

 

Step 4) Calculate _(adjusted)SS_total(Y)

 

Step 5) Calculate r_within²

Obtain r_within² for Y_within by first calculating SC_within

 

Step 6) Calculate _(adjusted)SS_within(Y)

 

Step 7) Calculate _(adjusted)SS_between(Y)

 

Step 8) Calculate the p Value

Arrange all of the above data on the ANOVA Excel output table and calculate the new p Value

Here is a detailed description of the performance of each step

 

Step 1) Run Single-Factor ANOVA on the Dependent Variable Data

Run Excel Single-Factor ANOVA on the Y (Dependent Variable) data in order to obtain SS_total(Y), SS_within(Y), and SS_between(Y)

The first step is to arrange the Dependent Variable data with each sample group in a different but contiguous (touching) column as shown. After the data is correctly arranged on the Excel worksheet, use the Excel data analysis tool ANOVA: Single-Factor to perform single-factor ANOVA on the two sample groups of Dependent data as follows:

(Click On Image To See a Larger Version)

 

(Click On Image To See a Larger Version)

SS_between(Y) = 6.05

SS_within(Y) = 662.5

SS_total(Y) = 668.55

 

Step 2) Run Single-Factor ANOVA on the Covariate Variable Data

Run Excel Single-Factor ANOVA on the X (covariate) data in order to obtain SS_total(X) and SS_within(X)

The first step is to arrange the Covariate Variable data with each sample group in a different but contiguous (touching) column as shown. After the data is correctly arranged on the Excel worksheet, use the Excel data analysis tool ANOVA: Single-Factor to perform single-factor ANOVA on the two sample groups of Covariate data as follows:

(Click On Image To See a Larger Version)

(Click On Image To See a Larger Version)

SS_within(X) = 788.9

SS_total(X) = 908.5

 

Step 3) Calculate R_total²

Calculate R_total² for Y_total. R_total² is derived from r_total, which is the overall correlation between X and Y

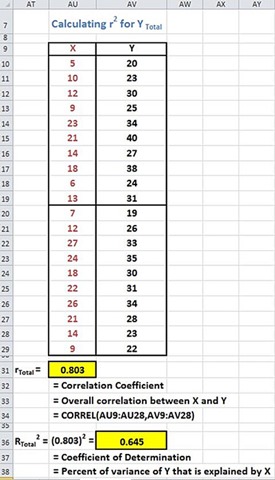
(Click On Image To See a Larger Version)

R_total² = 0.645

 

Step 4) Calculate _(adjusted)SS_total(Y)

 

(Click On Image To See a Larger Version)

 

Step 5) Calculate r_within²

Obtain r_within² for Y_within by first calculating SC_within

 

(Click On Image To See a Larger Version)

 

(Click On Image To See a Larger Version)

(Click On Image To See a Larger Version)

 

Step 6) Calculate _(adjusted)SS_within(Y)

 

(Click On Image To See a Larger Version)

 

Step 7) Calculate _(adjusted)SS_between(Y)

 

(Click On Image To See a Larger Version)

 

Step 8) Calculate the p Value

Arrange all of the above data on the ANOVA Excel output table and calculate the new p Value.

Calculate MS_between and MS_within from _(adjusted)SS_between(Y) , _(adjusted)SS_within(Y) , and the degrees of freedom of each.

Calculate the F Value from MS_between and MS_within.

Calculate the p Value from the F Value and both degrees of freedom.

(Click On Image To See a Larger Version)

 
(Click On Image To See a Larger Version)

The original ANOVA test did not detect a difference in monthly sales increases from either training method. This ANOVA was performed in Step 1 and produced a p Value = 0.68994.

ANCOVA did detect a significant difference in monthly sales increases between the two training methods after removing the effects of the Covariate variable (years of prior experience). The very low p Value = 0.00092 indicates that Training method A significantly outperformed Training Method B. The high r_within² indicates that the years of experience of each salesperson had a very substantial effect on the salesperson’s ability to translate either training program into increased sales following the training.

Derivation of the 8 Steps of ANCOVA

The most intuitive way to understand the derivation of the steps needed to perform ANCOVA is to work backwards from the very last step – the calculation of the p Value for the ANCOVA. This reverse derivation is performed as follows:

Calculating _adjusted p Value

The p Value for single-factor ANOVA is calculated in Excel as follows:

p Value = F.DIST.RT(F value, df_between, df_within)

The p Value for ANCOVA is the p Value of single-factor ANOVA adjusted by removing the effects of the Confounding Variable. This adjusted p Value is defined in Excel as follows:

_adjusted p Value = F.DIST.RT(_adjusted F value, _adjusted df_between, _adjusted df_within)

_adjusted df_between = df_between

There is no adjustment necessary for df_between because the number of groups has not changed from ANOVA to ANCOVA.

_adjusted df_within = df_within – 1

In ANCOVA the within-group degrees of freedom is reduced from ANOVA by 1 to account for the fact that the covariance portion of within-groups has been removed from the analysis.

Calculating _adjusted F Value

F Value = MS_between / MS_within

_adjusted F Value = _adjusted MS_between / _adjusted MS_within

Calculating _adjusted MS

MS_between = SS_between / df_between

_adjusted MS_between = _adjusted SS_between / _adjusted df_between

MS_within = SS_within / df_within

_adjusted MS_within = _adjusted SS_within / _adjusted df_within

We now need to calculate _adjusted SS_between and _adjusted SS_within to complete the derivation.

Calculating _adjusted SS_within

SS_total(Y) is found within the output of Excel single-factor ANOVA performed on the sample groups of the Dependent Variable Y, which is the Monthly Sales Increase.

r_XY = Correlation between the X-Y data pairs. X is the Covariate variable which is the Prior Years of Experience. Y is the Dependent variable, which is the Monthly Sales Increase.

r_XY = CORREL( X data array, Y data array)

R Square = (r_XY)² and represents the portion of total variance (SS_total) that is explained by the Dependent Variable Y. The following relationship is therefore correct:

SS_total(Y) = Portion of SS_total attributed to X = (r_XY)² * SS_total(Y)

_adjusted SS_total(Y) = SS_total(Y) - Portion of SS_total attributed to X

_adjusted SS_total(Y) = SS_total(Y) - (r_XY)² * SS_total(Y)

SS_total(Y) = SS_between(Y) + SS_within(Y)

_adjusted SS_total(Y) = _adjusted SS_between(Y) + _adjusted SS_within(Y)

_adjusted SS_within(Y) = SS_within(Y) – Portion of SS_within(Y) attributed to X

SS_within(Y) is found within the output of Excel single-factor ANOVA performed on the sample groups of the Dependent Variable Y, which is the Monthly Sales Increase.

Portion of SS_within(Y) attributed to X = r_within² * SS_within(Y)

r_within = SC_within / SQRT( SS_within(X) * SS_within(Y) )

This equation is derived as follows:

Correlation between X and Y = r_xy

r_xy = cor(x,y)

= cov(x,y) / σ_X σ_Y

= σ_XY / σ_X σ_Y

= σ_XY / SQRT( σ_XX * σ_YY )

= SC_total / SQRT( SS_total(X) * SS_total(Y) )

Because

σ_X = standard deviation of X

σ_Y = standard deviation of Y

σ_XY = cov(x,y)

σ_XX = Variance of X = SS_total(X) and is found in the output of Excel single-factor ANOVA performed on the sample groups of the Covariate Variable X, which is the Years of Prior Experience.

σ_YY = Variance of Y = SS_total(Y) and is found in the output of Excel single-factor ANOVA performed on the sample groups of the Dependent Variable Y, which is the Monthly Sales Increase.

Since we now have r_XY, we can now _adjusted SS_total(Y) calculate as follows:

_adjusted SS_total(Y) = SS_total(Y) - (r_XY)² * SS_total(Y)

Because of the above equation

r_xy = SC_total / SQRT( SS_total(X) * SS_total(Y) )

The following equation is valid:

r_within = SC_within / SQRT( SS_within(X) * SS_within(Y) )

In order to calculate r_within we still need to calculate SC_within

SC_within = SC_within(A) + SC_within(B)

A designates data associated with Training method 1

B designates data associated with Training method 2

SC_within = Covariance(X,Y) which is defined by the following formula:

cov(X,Y) = Σ (X_iY_i) - µ_Xµ_Y

cov(X,Y) = Σ (X_iY_i) – [ (ΣX_i)(ΣY_i) / N ]

SC_within = Σ (X_iY_i) – [ (ΣX_i)(ΣY_i) / N ]

SC_within(A) and SC_within(B) are therefore defined as follows:

SC_within(A) = Σ (X_AiY_Ai) – [ (ΣX_Ai)(ΣY_Ai) / N_A ]

SC_within(B) = Σ (X_BiY_Bi) – [ (ΣX_Bi)(ΣY_Bi) / N_B ]

We can now calculate the following:

SC_within = SC_within(A) + SC_within(B)

Which means we can now calculate the following:

r_within = SC_within / SQRT( SS_within(X) * SS_within(Y) )

Which allows us to calculate the following:

Portion of SS_within(Y) attributed to X = r_within² * SS_within(Y)

We can now calculate _adjusted SS_within(Y) as follows:

_adjusted SS_within(Y) = SS_within(Y) – Portion of SS_within(Y) attributed to X

Calculating _adjusted SS_between

_adjusted SS_total(Y) = _adjusted SS_between(Y) + _adjusted SS_within(Y)

_adjusted SS_between(Y) = _adjusted SS_total(Y) - _adjusted SS_within(Y)

Now that we have _adjusted SS_within(Y), _adjusted SS_between(Y), _adjusted df_within, and _adjusted df_between

We can calculate _adjusted MS_between and _adjusted MS_within as follows:

_adjusted MS_between = _adjusted SS_between / _adjusted df_between

_adjusted MS_within = _adjusted SS_within / _adjusted df_within

Now that we have _adjusted MS_between and _adjusted MS_within

We can calculate _adjusted F Value as follows:

_adjusted F Value = _adjusted MS_between / _adjusted MS_within

Now that we have _adjusted F Value, _adjusted df_between, and _adjusted df_within

We can calculate _adjusted p Value in Excel as follows:

_adjusted p Value = F.DIST.RT(_adjusted F value, _adjusted df_between, _adjusted df_within)

Calculating Effect Size in ANCOVA

Effect size is a way of describing how effectively the method of data grouping allows those groups to be differentiated. A simple example of a grouping method that would create easily differentiated groups versus one that does not is the following.

Imagine a large random sample of height measurements of adults of the same age from a single country. If those heights were grouped according to gender, the groups would be easy to differentiate because the mean male height would be significantly different than the mean female height. If those heights were instead grouped according to the region where each person lived, the groups would be much harder to differentiate because there would not be significant difference between the means and variances of heights from different regions.

Because the various measures of effect size indicate how effectively the grouping method makes the groups easy to differentiate from each other, the magnitude of effect size tells how large of a sample must be taken to achieve statistical significance. A small effect can become significant if a larger enough sample is taken. A large effect might not achieve statistical significance if the sample size is too small.

The two most common measures of effect size of one-way ANCOVA are the following:

Eta Square (η²)

(Greek letter “eta” rhymes with “beta”) Eta square quantifies the percentage of variance in the dependent variable (the variable that is measured and placed into groups) that is explained by the independent variable (the method of grouping). If eta squared = 0.35, then 35 percent of the variance associated with the dependent variable is attributed to the independent variable (the method of grouping).

Eta square provides an overestimate (a positively-biased estimate) of the explained variance of the population from which the sample was drawn because eta squared estimates only the effect size on the sample. The effect size on the sample will be larger than the effect size on the population. This bias grows smaller is the sample size grows larger.

Eta square is affected by the number and size of the other effects.

η² = SS_{Between_Groups} / SS_Total These two terms are part of the ANOVA calculations found in the Single-factor ANOVA output.

Jacob Cohen in his landmark 1998 book Statistical Analysis for the Behavior Sciences proposed that effect sizes could be generalized as follows:

η² = 0.01 for a small effect. A small effect is one that not easily observable.

η² = 0.05 for a medium effect. A medium effect is more easily detected than a small effect but less easily detected than a large effect.

η² = 0.14 for a large effect. A large effect is one that is readily detected with the current measuring equipment.

Eta squared is sometimes called the nonlinear correlation coefficient because it provides a measure of strength of the curvilinear relationship between the dependent and independent variables. If the relationship is linear, eta squared will have the same value as r squared.

Eta squared is calculated in Excel with the formula

η² = SS_{Between_Groups} / SS_Total

Omega Squared (ώ²)

Omega squared is an estimate of the population’s variance that is explained by the treatment (the method of grouping).

Omega squared is less biased (but still slightly biased) than eta square and is always smaller the eta squared because eta squared overestimates the explained variance of the population from which the sample was drawn. Eta squared estimates only the effect size on the sample. The effect size on the sample will be larger than the same effect size on the population.

Magnitudes of omega squared are generally classified as follows: Up to 0.06 is considered a small effect, from 0.06 to 0.14 is considered a medium effect, and above 0.14 is considered a large effect. Small, medium, and large are relative terms. A large effect is easily discernible but a small effect is not.

Omega Square is implemented in Excel as follows:

After the adjusted ANCOVA table is created for the dependent variable (Measured Post-Training Sales Increase), both of the preceding Effect Size formulas can be quickly calculated with figures taken directly from the adjusted ANCOVA table as follows:

(Click On Image To See a Larger Version)

An eta-square value of 0.448 would be classified as a very large size effect.

An omega-square value of 0.442 would also be classified as a very large size effect.

A large effect is one that is readily observable (after the effects of the Covariate variable have been removed).

 

Excel Master Series Blog Directory

 

Click Here To See a List Of All

Statistical Topics And Articles In

This Blog

 

You Will Become an Excel Statistical Master!