Thursday, May 29, 2014

Simple Linear Regression in 7 Steps in Excel 2010 and Excel 2013

This is one of the following seven articles on Simple Linear Regression in Excel

Overview of Simple Linear Regression in Excel 2010 and Excel 2013

Complete Simple Linear Regression Example in 7 Steps in Excel 2010 and Excel 2013

Residual Evaluation For Simple Regression in 8 Steps in Excel 2010 and Excel 2013

Residual Normality Tests in Excel – Kolmogorov-Smirnov Test, Anderson-Darling Test, and Shapiro-Wilk Test For Simple Linear Regression

Evaluation of Simple Regression Output For Excel 2010 and Excel 2013

All Calculations Performed By the Simple Regression Data Analysis Tool in Excel 2010 and Excel 2013

Prediction Interval of Simple Regression in Excel 2010 and Excel 2013

 

Complete Example of

Simple Linear Regression

in 7 Steps  in Excel

A company has a large plastic injection molding machine. The company would like to create an equation that will calculate the number of identical plastic parts that would be produced for a specified quantity of input plastic pellets.

The company conducted 21 independent production runs on the machine. In each case a different-sized batch of plastic pellets was input into the machine and the total number of identical plastic parts produced from each batch was recorded.

If the relationship between quantity of input plastic pellets in each batch and the number of parts produced from each batch is linear, calculate the equation that describes that relationship.

It is important to note that all trial runs were performed as identically as possible. The same operator ran the machine on each trial run at approximately the same time during a shift. The machine was calibrated to the same settings and cleaned prior to each trial run and input plastic pellets from the same batch were used in all 21 trial runs.

The data from the 21 trial runs are as follows:

regression, excel, excel 2010, excel 2013,statistics,residuals
(Click On Image To See a Larger Version)

 

Excel Regression Step 1 –

Remove Extreme Outliers

Calculation of the mean is one of the fundamental computations when performing linear regression analysis. The mean is unduly affected by outliers. Extremely outliers should be removed before beginning regression analysis. Not all outliers should be removed. An outlier should be removed if it is obviously extremely and inconsistent with the remainder of the data.

At this point in the beginning of the analysis, the objective is to remove outliers that are obviously extreme. After Excel has performed the regression and calculated the residuals, further analysis will be performed to determine if any of the data points can also be considered outliers based upon any unusually large residual terms generated. A data point is often considered to be an outlier if its residual value is more than there standard deviations from the mean of the residuals.

 

Sorting the Data To Quickly Spot Extreme Outliers

An easy way to quickly spot extreme outliers is to sort the data. Extremely high or low outlier values will appear at the ends of the sort. A convenient, one-step method to sort a column of data in Excel is shown here.

The formula is cell D3 is the following:

=IF($A3=””,””,LARGE($A$3:$A$23,ROW()-ROW($C$2)))

Copy this formula down as shown to create a descending sort of the data in cells A3 to A23.

Exchanging the word SMALL for LARGE would create an ascending sort instead of the descending sort performed here.

regression, excel, excel 2010, excel 2013,statistics,residuals(Click On Image To See a Larger Version)

The lowest Y value, 9, is obviously an extreme outlier and is very different than the rest of the data. The cause of this extreme outlier value is not known. Perhaps something unexpected happened during this production run? It is clear that this value should be removed from the analysis because it would severely skew the final result.

Removing this outlier from the data produces this set of 20 data samples:

regression, excel, excel 2010, excel 2013,statistics,residuals
(Click On Image To See a Larger Version)

 

Excel Regression Step 2 –

Create a Correlation Matrix

This step is only necessary when performing multiple regression, i.e., linear regression that has more than one independent variable, not single variable regression as we are doing here. The purpose of this step is to identify independent variables that are highly correlated. Different input variables that are highly correlated cause an error called multicollinearity. There is no need to check for correlated independent variables when performing single-variable regression as we are doing here because there is only one independent variable. This step should always be carried out when performing multiple regression. When highly correlated pairs of independent variables are found, one of the variables of the pair should be removed from the regression.

 

Excel Regression Step 3 –

Scale Variables If Necessary

All variables should be scaled so that each has a similar number of decimal places beyond zero. This limits rounding error and also insures that the slope of the fitted line will be a convenient size to work with and not too large or too small.

The weight of the input pellets is measured in grams. If these weights were specified in kilograms, both variables would be presented in much closer scales. Changing the scale of the incoming pellet weight from grams to kilograms provides the following properly-scaled data:

regression, excel, excel 2010, excel 2013,statistics,residuals
(Click On Image To See a Larger Version)

 

Excel Regression Step 4 –

Plot the Data

The purpose of this step is to check for linearity. Each independent variable should be plotted against the dependent variable in a scatterplot graph. Linear regression should only be performed if linear relationships exist between the dependent variable and each of the input variables. An Excel X-Y scatterplot of the two X-Y variables is shown as follows. The relationship appears to be a linear one.

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

 

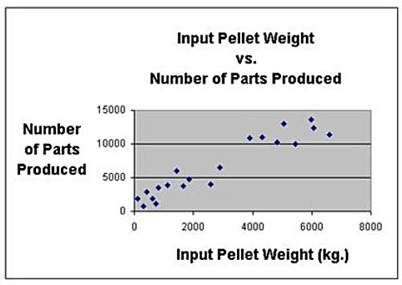
Excel Regression Step 5 –

Run the Regression Analysis

in Excel

Below is the Regression dialogue box with all necessary information filled in. Many of the required regression assumptions concerning the Residuals have not yet been validated. At this point the regression is being run in Excel to calculate the Residuals in order to analyze them. Further analysis of the Excel regression output should take place only after linear regression’s required assumptions concerning the Residuals have been evaluated.

Calculating the Residuals as part of the Excel regression output is specified in the Excel regression dialogue box as follows:

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

It should be noted that the Residuals are sometimes referred to as the Error terms. The checkbox next to Residuals should be checked in order to have Excel automatically calculate the residual for each data point. The residual is the difference between the actual data point and its value as predicted by the regression equation. Analysis of the residuals is a very important part of linear regression analysis because a number of required assumptions are based upon the residuals.

The checkbox next to Standardized Residuals should also be checked. If this is checked, Excel will calculate the number of standard deviations that each residual value is from the mean of the residuals. Data points are often considered outliers if their residual values are located more than three standard deviations from the residual mean.

The checkbox next to Residual Plots should also be checked. This will create graphs of the residuals plotted against each of the input (independent) variables. Visual observation of these graphs is an important part of evaluating whether the residuals are independent. If the residuals show patterns in any graph, the residuals are considered to not be independent and the regression should not be considered valid. Independence of the residuals is one of linear regression’s most important required assumptions.

The checkbox next to Line Fit plots should be checked as well. This will produce graphs of the Y Values plotted against each X value in a separate graph. This provides visual analysis of the spread of each input (X) variable and any patterns between any X variable the output Y variable.

The checkbox for the Normal Probability Plot was not checked because that produces a normal probability plot of the Y data (the dependent variable data). A normal probability plot is used to evaluate whether data is normally-distributed. Linear regression does not require the independent or dependent variable data be normally-distributed. Many textbooks incorrectly state that the dependent and/or independent data need to be normally-distributed. This is not the case.

Linear regression does however require that the residuals be normally-distributed. A normal probability plot of the residuals would be very useful to evaluate the normality of the residuals but is not included as a part of Excel’s regression output.

A normal probability plot of the Y data does not provide any useful information and the checkbox that would produce that graph is therefore not checked. It is unclear why Excel includes that functionality with its regression data analysis tool.

Those settings shown in the preceding Excel regression dialogue box produce the following output:

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

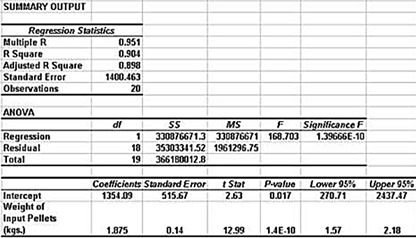
The Excel regression output includes the calculation of the Residuals as specified. Linear regression’s required assumptions regarding the Residuals should be evaluated before analyzing any other part of the Excel regression output. The required Residual assumptions must be verified before the regression output is considered valid.

The Residual output includes each Dependent variable’s predicted value, its Residual value (the difference between the predicted value and the actual value), and the Residual standardized value (the number of standard deviations that the Residual value is from the mean of the Residual values). This Residual output is shown as follows:

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

The follow graphs were also generated as part of the Excel regression output:

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

 

Excel Regression Step 6 –

Evaluate the Residuals

The purpose of Residual analysis is to confirm the underlying validity of the regression. Linear regression has a number of required assumptions about the residuals. These assumptions should be evaluated before continuing the analysis of the Excel regression output. If one or more of the required residual assumptions are shown to be invalid, the entire regression analysis might be considered, at best, questionable or, at worst, invalid. The residuals should therefore be analyzed first before analyzing any other part of the Excel regression output.

The Residuals are sometimes called the Error Terms. The Residual is the difference between an observed data value and the value predicted by the regression equation. The formula for the Residual is as follows:

Residual = Yactual – Yestimated

 

Linear Regression’s Required Residual Assumptions

Linear regression has several required assumptions regarding the residuals. These required residual assumptions are as follows:

1) Outliers have been removed.

2) The residuals must be independent of each other. They must not be correlated with each other.

3) The residuals should have a mean of approximately 0.

4) The residuals must have similar variances throughout all residual values.

5) The residuals must be normally-distributed.

6) The residuals may not be highly correlated with any of the independent (X) variables.

7) There must be enough data points to conduct normality testing of residuals.

Residual Analysis will be performed in a blog article following this one.

 

Excel Regression Step 7 –

Evaluate the Excel Regression

Output

The Excel regression output from this example shown below will be evaluated in a blog article shortly following this one.

regression, excel, excel 2010, excel 2013,statistics,residuals (Click On Image To See a Larger Version)

 

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

 

Posted by at

1 comment:

  1. marksonAugust 21, 2019 at 3:15 AM

    These gatherings are magnificent with regards to open source information investigate.machine learning course

    ReplyDelete

Subscribe to: Post Comments (Atom)