Two-Factor ANOVA With Replication in 5 Steps in Excel 2010 and Excel 2013

This is one of the following seven articles on Two-Factor ANOVA With Replication in Excel

Two-Factor ANOVA With Replication in 5 Steps in Excel 2010 and Excel 2013

Variance Tests: Levene’s and Brown-Forsythe For 2-Factor ANOVA in Excel 2010 and Excel 2013

Shapiro-Wilk Normality Test in Excel For 2-Factor ANOVA With Replication

2-Factor ANOVA With Replication Effect Size in Excel 2010 and Excel 2013

Excel Post Hoc Tukey’s HSD Test For 2-Factor ANOVA With Replication

2-Factor ANOVA With Replication – Test Power With G-Power Utility

Scheirer-Ray-Hare Test Alternative For 2-Factor ANOVA With Replication

 

Two-Factor ANOVA With

Replication in 5 Steps in

Excel

Two-factor ANOVA with replication is used to determine if either of two categorical factors and/or the interaction between these two factors has had a significant effect on a data set of continuous data.

Two-factor ANOVA with replication is useful in the following two circumstances:

 

1) Determining if either of two categorical factors has independently affected a data set in a significant way.

The data set is divided into horizontal groups that are each affected by a different level of one categorical factor. The same data set is also simultaneously divided into vertical groups that are each affected by a different level of another categorical factor. An example of a data set that is arranged for two-factor ANOVA with replication analysis is as follows:

 
(Click On Image To See a Larger Version)

The test for main effects of each of the two factors is very similar to main effects test of the one factor in single-factor ANOVA. The main effects test for each of the two factors determines whether there is a significant difference between the means of the groups (the levels) within that factor. Factor 1’s main effect test determines if there is a significant difference between the means of Levels 1, 2, and 3 of Factor 1. Factor 2’s main effects test determines if there is a significant difference between the means of Levels 1 and 2 of Factor 2.

 

2) Determining if the interaction between the two categorical factors has significantly affected a data set.

The interaction test determines whether data values across the levels of one factor vary significantly at different levels of the other factor. This test determines whether the levels of one factor have different effects on the data values across the levels of the other factor. It determines whether there is interaction between Factor 1 and Factor 2, that is, between rows and columns. Ultimately this test determines whether the differences between data observations in columns vary from row to row and the differences between data observations vary from column to column.

 

Independent Variables vs. Dependent Variables

The two factors and their levels are categorical. These two factors are sometimes referred to as the independent variables of Two-Way ANOVA. The dependent variable contains the values of the data observations in the ANOVA table. The dependent variable is a continuous variable.

 

Two-Way ANOVA

Two-way ANOVA means that there are two factors that are being evaluated. Each factor has at least two or more levels. One of the factors has its levels distributed in columns. Each data column contains all of the data observations of one of that factor’s levels. The other factor has its levels distributed in rows. Each data row contains all of the data observations of one of that factor’s levels.

 

Balanced Two-Way ANOVA With Replication

Replication in two-way ANOVA occurs when there are multiple instances of data observations for each combination of levels between the two factors. Each unique combination of levels of the two factors is called a treatment cell. It is important to note that only one of the two factors will always be replicated and the other factor will never be replicated in the treatment cells. In the example provided here, each treatment cell contains four data observations that are replications of Factor 1.

It is also important to note that the replication occurs the same number of times at all combinations of levels. In the example shown here, each combination of levels of Factors 1 and 2 contains four data observations of the same level of Factor 1. This is called “balanced” ANOVA. Balanced ANOVA means that each treatment cell (each unique combination of levels of Factors 1 and 2) has one of the factors replicated the same number of times.

ANOVA can be performed on unbalanced data but it is significantly more complicated and will not be discussed here. It is always a good idea to design two-factor ANOVA with replication testing to have balanced treatment cells. It should be noted that single-factor ANOVA can be performed without any additional complication when treatments cells (data groups) have different sizes.

ANOVA = Analysis of Variance

ANOVA stands for Analysis of Variance. ANOVA determines whether or not all of the sample groups being compared in a single F test are likely to have come from the same population by comparing the variance between sample groups to the variance within the sample groups.

Two-factor ANOVA represents groupings of data observations that are each described by two categorical variables and one continuous variable. The value of each object’s categorical variables determines into which group (treatment cell) the data observation is placed. A treatment cell is a unique combination of levels of the two factors. Two-Way ANOVA with one factor that has two levels and a second factor that has three levels would have a total of six unique treatment cells.

The number of data observations in each treatment cells depends on how much replication has occurred in the ANOVA test. Two-Way ANOVA Without Replication has a single data observation in each treatment cell. Two-Way ANOVA with one factor replicated twice has two data observations in each treatment cell. The example shown in this section has one factor replicated four times and therefore has four data observations in each treatment cell. Note that this ANOVA example is balanced because each treatment cell contains the same number of data observations (four) that are replications of the same factor.

The Independent and Dependent Variables of ANOVA

The categorical variables are sometimes referred to as the independent variables of the ANOVA while the continuous variable is sometimes referred to as the dependent variable of the ANOVA. In the case of Two-Factor ANOVA, the independent variables predict which unique group (treatment cell) that each data observation’s continuous value or measurement will be placed. This independent-dependent relationship is different from that in regression because the independent variable does not predict the value of the dependent variable, only the group (factor level) into which data observation will be placed.

 

Two-Way ANOVA With Replication Performs Three F Tests

The three separate F Tests performed are the following:

Factor 1 Main Effects F Test

This F Test determining whether at least one level of the Factor 1 groupings of the data set has a significantly different mean than the other Factor 1 levels. This is a Main Effects test.

 

Factor 2 Main Effects F Test

This F Test determining whether at least one level of the Factor 2 groupings of the data set has a significantly different mean than the other Factor 2 levels. This is a Main Effects test.

 

Factor 1 and 2 Interaction Effects F Test

this F Test to determining whether any level of Factor 1 interacts with Factor 2 to create significantly different mean values in treatment cells across the Factor 2 levels. This is an Interaction Test.

Each of these three F Tests produces its own p value and a result that is reported separately from the other two F Tests.

 

Requirements of Each F Test

All groups that are part of one F Test should be drawn from normally distributed populations that have similar variances. This means that all data groups in one F Test must have similar variances and be normally distributed. Only data groups that are being used in the same F Test are required to have similar variances. All data groups for all F Tests must be normally distributed. The three F Tests of Two-Factor ANOVA With Replication are valid only if the following conditions are met:

 

Factor 1 Main Effects F Test Requirement

All data groupings for Factor 1 (each Factor 1 level is its own data grouping) must have similar variances and be normally distributed.

 

Factor 2 Main Effects F Test Requirement

All data groupings for Factor 2 (each Factor 2 level is its own data grouping) must have similar variances and be normally distributed.

 

Factor 1 and 2 Interaction Effects F Test Requirement

If the two points above are true, then all interaction groupings (the unique treatment cells) will have similar variance and be normally distributed.

Note that the variances of the groups within each F Test need to similar, not the same as is often quoted in statistics texts. A rule-of-thumb is that the groups of an F Test are considered to have similar variances if the standard deviation of any group is no more than twice as large as the standard deviation of any other group in that F Test.

Group variances for each F Test will be compared in this section using both Levene’s test and the Brown-Forsythe test. These are widely-used hypothesis tests that indirectly determine whether group variances are different are significantly different.

Normality testing will be conducted on all groups of all F Tests in this section using the well-known Shapiro-Wilk normality test.

 

Alternative Test When Data Are Normally Distributed

ANOVA is a parametric test because one of ANOVA’s requirements is that the data in each sample group are normally distributed. ANOVA is relative robust against minor deviations from normality. When normality of sample group data cannot be confirmed or if the sample data is ordinal instead of continuous, a relatively unknown but very useful nonparametric test called the Scheirer-Ray-Hope test should be substituted for Two-Factor ANOVA With Replication. This test will be performed on the data at the end of this section.

Ordinal data are data whose order matter but the specific distances between units is not measurable. Customer-rating survey data and Likert scales data can be examples of ordinal data. These types of data can, however, be treated as continuous data if distances between successive units are considered equal.

The nonparametric Friedman test is sometimes mentioned as a substitute for Two-Way ANOVA With Replication but this is incorrect. The Friedman test is a nonparametric substitute for Repeated-Measure ANOVA but not for Two-Way ANOVA With Replication.

 

Null and Alt. Hypotheses For 2-Way ANOVA W/Rep.

Each of the three F Tests has its own Null and Alternative Hypotheses.

Null and Alternative Hypotheses for the Two Main Effects F Tests

The Null Hypothesis for the F Test that compares the means of the Factor 1 levels states that all of the means are the same.

The Null Hypothesis for the F Test that compares the means of the Factor 2 levels states that all of the means are the same.

This would be written as follows:

Null Hypothesis = H₀: µ₁ = µ₂ = … = µ_k (k equals the number of sample groups or levels in each factor)

Note that Null Hypothesis is not referring to the sample means, s₁ , s₂ , … , s_k, but to the population means, µ₁ , µ₂ , … , µ_k. Each of these two F Tests determine whether all of the data groups in a single F Test could have come from the same population.

The Alternative Hypothesis for ANOVA states that at least one sample group in the F Test is likely to have come from a different population. The F Tests do not clarify which groups are different or how large any of the differences between the groups are. This Alternative Hypothesis for an F Test only states whether at least one sample group in that F Test is likely to have come from a different population.

 

Null and Alternative Hypotheses for the Interaction Effect F Tests

The Null Hypothesis for the F Test that compares the interaction effect states that there is no interaction between Factor 1 and Factor 2, that is, between rows and columns. This Null Hypothesis states that the differences between data observations in columns do not vary from row to row and the differences between data observations do not vary from column to column.

The Alternative Hypothesis for each of the three F Tests states that its Null Hypothesis is not true. Keep in mind that a hypothesis test never accepts or rejects an alternative hypothesis: a hypothesis test can only reject or fail to reject its Null Hypothesis. Rejection of the Null Hypothesis is however usually deemed as being supportive of the Alternative Hypothesis stating that there is a difference in what is being compared.

 

Two-Factor ANOVA Should Not Be Done By Hand

Excel provides an excellent ANOVA tool that can perform Single-factor or two-Factor ANOVA with equal ease. The section in this manual covering single-factor ANOVA has the example recreated with all of the individual calculations that go into ANOVA. This will not be done for two-factor ANOVA because that would not, in this author’s view, provide additional insight into two-factor ANOVA because its calculations are very numerous and tedious.

The best way to understand Two-Factor ANOVA with replication is to perform an example as follows:

 

Two-Factor ANOVA With

Replication Example in Excel

The two factors of this ANOVA test will generically be called Factor 1 and Factor 2. Factor 1 will have three levels and Factor 2 will have 2 levels. Each level of Factor 1 will be replicated four times.

The three levels of Factor 1 are labeled as follows:

Factor 1 Level 1

Factor 1 Level 2

Factor 1 Level 3

The two levels of Factor 2 are labeled as follows:

Factor 2 Level 1

Factor 2 Level 2

The generic labels were retained through the entire example to provide additional clarity and ease of interpretation of the output. The data will be arranged as follows so they can be processed in Excel:

 
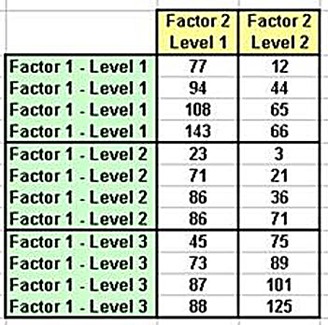
(Click On Image To See a Larger Version)

This example could have been something similar to the following:

Three groups of eight people simultaneously underwent training programs. Each of the three training programs was different. Each group contains four men and four women. All people in all groups are judged to have similar abilities. At the end of the training program, all eight people in each group took the same test to evaluate comprehension of the training topics.

The three levels of Factor 1 would, in this case, would specify which training program each person had undergone. The two levels of Factor 2 would specify the gender of each person.

Arranging the data in table as shown would allow for Two-Factor ANOVA With Replication to determine the following:

1) Whether the training programs made a significant difference in the test scores.

2) Whether test scores were significantly different between gender.

3) Whether there was interaction between training program type and gender. In other words, whether participants of one gender seemed to perform better or worse in at least one training program than participants of the other gender did.

 

ANOVA Step 1 – Arrange the Data Properly

Typically the data is provided in the manner shown as follows. Each data observation is listed on a separate row along with its respective level of the other two factors.

(Click On Image To See a Larger Version)

To perform Two-Factor ANOVA with replication in Excel, the data needs to be arranged in rows and columns as follows:

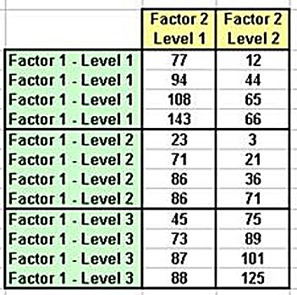
(Click On Image To See a Larger Version)

The quickest way to arrange the data correctly is to sort the rows of data by the two factors. The factor that will not be replicated should be sorted as a primary sort. Levels of this data will wind up in separate columns. The factor that will be replicated should be the secondary sort. Levels of this data will wind up in blocks of rows as just shown.

(Click On Image To See a Larger Version)

Second, create the framework into which the sorted data will be placed as follows:

(Click On Image To See a Larger Version)

Third, paste the data into the respective columns.

(Click On Image To See a Larger Version)

Fourth and finally, outline each treatment cell as follows. Each treatment cell is a unique combination of levels of both factors and contains four data observations. The data should be balanced meaning that every treatment cell has the same number of data observations.

(Click On Image To See a Larger Version)

 

ANOVA Step 2 – Evaluate Extreme Outliers

Calculation of the mean is one of the fundamental computations when performing ANOVA. The mean is unduly affected by outliers. Extremely outliers should be removed before ANOVA. Not all outliers should be removed. An outlier should be removed if it is obviously extreme and inconsistent with the remainder of the data.

Outlier evaluation needs to be carefully performed before or during data collection, not after. Two-Way ANOVA With Replication requires that the data be balanced. Individual data observations cannot simply be discarded or there will be a hole in the data and the data will no longer be balanced. Note that Single-Factor ANOVA can easily be performed on unbalanced data, but not Two-Factor ANOVA With Replication. This type of ANOVA can be done with unbalanced data but it is significantly more complicated and cannot be performed by the data analysis tool in Excel.

 

ANOVA Step 3 – Verify Required Assumptions

Two-Factor ANOVA With Replication Required Assumptions

Two-Factor ANOVA With Replication has six required assumptions whose validity should be confirmed before this test is applied. The six required assumptions are the following:

1) Independence of Sample Group Data. Sample groups must be differentiated in such a way that there can be no cross-over of data between sample groups. No data observation in any sample group could have been legitimately placed in another sample group. No data observation affects the value of another data observation in the same group or in a different group. This is verified by an examination of the test procedure.

2) Sample Data Are Continuous. Sample group data (the dependent variable’s measured value) can be ratio or interval data, which are the two major types of continuous data. Data observation values cannot be nominal or ordinal data, which are the two major types of categorical data.

3) Independent Variables Are Categorical. The determinant of which group each data observation belongs to is a categorical, independent variable. ANOVA uses two categorical variables that each have at least two levels. All data observations associated with each variable level represent a unique data group and will occupy a separate column or row on the Excel worksheet.

4) Extreme Outliers Removed If Necessary. ANOVA is a parametric test that relies upon calculation of the means of sample groups. Extreme outliers can skew the calculation of the mean. Outliers should be identified before sampling. Occasional outliers are to be expected in normally distributed data but all outliers should be evaluated. Removing outliers after sampling can cause the data to be unbalanced (sample groups having different numbers of samples).

5) Normally Distributed Data In All Sample Groups. Each of the three F Tests of Two-Factor ANOVA has the required assumption the data from each sample group in that F Test comes from a normally distributed population. Each of the two F Tests that are main effects tests for the two factors should have their sample groups evaluated for normality. If all of the sample groups in the two F Tests are normally distributed, the sample groups for the interaction F Test will also be normally distributed.

Normality testing becomes significantly less powerful (accurate) when a group’s size fall below 20. An effort should be made to obtain group sizes that exceed 20 to ensure that normality tests will provide accurate results. The F Tests in ANOVA are somewhat robust to minor deviations from normality.

6) Relatively Similar Variances In All Sample Groups In Each F Test. Single-Factor ANOVA requires that sample groups are obtained from populations that have similar variances.

Each of the three F Tests of Two-Factor ANOVA has the required assumption that all sample groups in that specific F Test have similar variances. Each of the two F Tests that are main effects tests for the two factors should have their sample groups evaluated for homoscedasticity (similarity of variances). If all of the sample groups in the each F Tests have similar variances, the sample groups for the interaction F Test will also have similar variances. Note that variances only have to be similar in groups of a single F Test. All data groups that are the levels from one factor must have similar variances. Levels of one factor do not have to have similar variances to levels of the other factor though. The requirement is that sample groups for a single F Test have similar variances.

This requirement actually states that the populations from which the sample are drawn must have equal variances. Normally the population variances so the sample groups themselves must be tested for variance equality. The variances do not have to be exactly equal but do have to be similar enough so the variance testing of the sample groups, which are hypothesis tests, will not detect significant differences.

Variance testing becomes significantly less powerful (accurate) when a group’s size fall below 20. An effort should be made to obtain group sizes that exceed 20 to ensure that variance tests will provide accurate results.

 

Determining If Sample Groups Are Normally-Distributed

There are a number of normality test that can be performed on each group’s data. The normality test that is preferred because it is considered to be more powerful (accurate) than the others, particularly with smaller sample sizes is the Shapiro-Wilk test. this test will be performed onthesample data in a blog article shortly following this one.

 

Determining If Sample Groups Have Similar Variances

Each of the three F Tests of Two-Factor ANOVA With Replication requires that the variances of all sample groups in the same F Test be similar. Sample groups that have similar variances are said to be homoscedastistic. Sample groups that have significantly different variances are said to be heteroscedastistic.

A rule-of-thumb is as follows: Variances are considered similar if the standard deviation of any one group is no more than twice as large as the standard deviation of any other group. This is equivalent to stating that no data group’s variance can be more than four times the variance of another data group in the same F Test. That is the case here as the following are true for the levels of Factor 1 and Factor 2:

Variance tests Levene’s Test and the Brown-Forsythe Test will be performed on the sample data in a blog article shortly following this one.

 

Step 4 – Run the Two-Factor ANOVA With Replication Tool in Excel

ANOVA tools can be found in Excel 2007 and later by clicking the Data Analysis link located under the Data tab. In Excel 2003, the Data Analysis link is located in the Tool drop-down menu. Clicking Anova: Two-Factor With Replication brings up the Excel dialogue box for this tool.

The data need to be arranged in contiguous (columns touching with the rows correctly lined up) columns.

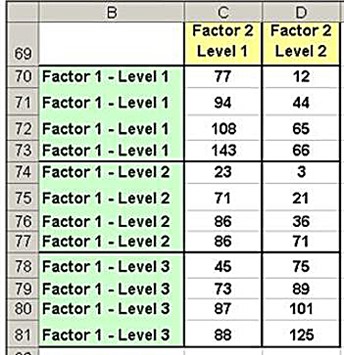
(Click On Image To See a Larger Version)

The completed dialogue box for this ANOVA test and data set would appear as follows:

 (Click On Image To See a Larger Version)

Hitting OK runs the tools and produces the following output:

 (Click On Image To See a Larger Version)

 

Step 5 – Interpret the Excel Output

Two-Way ANOVA With Replication Involves Three Separate F Tests. Each of these three F Tests produces its own p value and a result that is reported separately from the other two F Tests. Results of an F Test are deemed to be significant if the p Value generated by that F test is smaller than the designated Level of Significance (α is usually set of 0.05). A significant result is one in which observed differences have only a small chance of being random results. For example, if one of the Main Effects F Tests produces a significant result (the p Value is smaller than α) then at least one of the means of the level groups of that factor is different than the means of the other level data groups.

Those three separate F Tests are the following:

Main Effects F Test for Factor 1 - An F Test determining whether at least one level of the Factor 1 groupings of the data set has a significantly different mean than the other Factor 1 levels. This is a Main Effects test for Factor 1.

Main Effects F Test for Factor 2 - An F Test determining whether at least one level of the Factor 2 groupings of the data set has a significantly different mean than the other Factor 2 levels. This is a Main Effects test for Factor 2.

 

Main Effects F Test for Factor 1

This F Test has produced a p Value of 0.0333. At a Level of Significance (alpha) of 0.05, this F Test has produced a significant result because the generated p Value is smaller than the alpha level of 0.05. This result indicates at least 95 percent certainty that the mean at least one of the level data groups is different than means of the other level data groups of Factor 1. That can be stated equivalently by saying that there is less than a 5 percent chance that the detected difference is merely a random result of the sample taken and not real.

An F Test is an omnibus test meaning that it can detect significant difference(s) between the means but not the location of the significant difference(s) if there are more than two sample groups in the F Test. A post hoc test called Tukey’s HSD test will be performed to determine which differences between the means of Factor 1’s level groups are significant.

 

Main Effects F Test for Factor 2

This F Test has produced a p Value of 0.0442. At a Level of Significance (alpha) of 0.05, this F Test has produced a significant result because the generated p Value is smaller than the alpha level of 0.05. This result indicates at least 95 percent certainty that the mean at least one of the level data groups is different than means of the other level data groups of Factor 1. That can be stated equivalently by saying that there is less than a 5 percent chance that the detected difference is merely a random result of the sample taken and not real.

An F Test is an omnibus test meaning that it can detect difference(s) but not the location of the difference(s) if there are more than two sample groups in the F Test. In this case there are only two levels in Factor 2. The significant result of this F Test indicates the difference between those two levels is significant. Post hoc testing is not needed because the location of the significant difference is already known since there is only one difference.

 

Interaction Effects F Test for Factors 1 and 2

An F Test to determining whether any level of Factor 1 interacts with any level of Factor 2 to create significantly different mean values in treatment cells across the Factor 2 levels. This F Test analyses whether the systematic differences of means of treatment cells along rows vary at different column levels and vice versa. This is an Interaction Test.

This F Test has produced a p Value of 0.0142. At a Level of Significance (alpha) of 0.05, this F Test has produced a significant result because the generated p Value is smaller than the alpha level of 0.05. This result indicates at least 95 percent certainty that there is interaction between Factor 1 and Factor 2. That can be stated equivalently by saying that there is less than a 5 percent chance that the detected interaction is merely a random result of the sample taken and not real.

Post hoc testing would not be the most intuitive method to determine where the significant interactions occur. These differences will be most prominently displayed on a line graph connecting the means of treatment cells. A line graph of two-factor ANOVA will produce two line graphs that are next to each other. The greater the difference in the slopes of these lines, the more interaction between the Factors has occurred. The closer the two lines are to being parallel, the less interaction has occurred between the two factors. This graph will shortly be created and explained.

 

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

• Histograms in Excel
  • Creating a Histogram With the Histogram Data Analysis Tool in Excel
  • Creating an Automatically Updating Histogram in 7 Steps in Excel With Formulas and a Bar Chart
• Bar Chart in Excel
  • Creating a Bar Chart in 7 Steps in Excel 2010 and Excel 2013
• Combinations & Permutations in Excel
  • Combinations in Excel 2010 and Excel 2013
  • Permutations in Excel 2010 and Excel 2013
• Normal Distribution in Excel
  • Overview of the Normal Distribution
  • Normal Distribution’s PDF (Probability Density Function) in Excel 2010 and Excel 2013
  • Normal Distribution’s CDF (Cumulative Distribution Function) in Excel 2010 and Excel 2013
  • Solving Normal Distribution Problems in Excel 2010 and Excel 2013
  • Overview of the Standard Normal Distribution in Excel 2010 and Excel 2013
  • An Important Difference Between the t and Normal Distribution Graphs
  • The Empirical Rule and Chebyshev’s Theorem in Excel – Calculating How Much Data Is a Certain Distance From the Mean
  • Demonstrating the Central Limit Theorem In Excel 2010 and Excel 2013 In An Easy-To-Understand Way
• t-Distribution in Excel
  • Overview of the t- Distribution
• Binomial Distribution in Excel
  • Overview of the Binomial Distribution in Excel 2010 and Excel 2013
  • Solving Problems With the Binomial Distribution in Excel 2010 and Excel 2013
  • Normal Approximation of the Binomial Distribution in Excel 2010 and Excel 2013
  • Distributions Related to the Binomial Distribution
• z-Tests in Excel
  • Overview of Hypothesis Tests Using the Normal Distribution in Excel 2010 and Excel 2013
  • One-Sample z-Test in 4 Steps in Excel 2010 and Excel 2013
  • 2-Sample Unpooled z-Test in 4 Steps in Excel 2010 and Excel 2013
  • Overview of the Paired (Two-Dependent-Sample) z-Test in 4 Steps in Excel 2010 and Excel 2013
• t-Tests in Excel
  • Overview of t-Tests: Hypothesis Tests that Use the t-Distribution
  • 1-Sample t-Tests in Excel
    • 1-Sample t-Test in 4 Steps in Excel 2010 and Excel 2013
    • Excel Normality Testing For the 1-Sample t-Test in Excel 2010 and Excel 2013
    • 1-Sample t-Test – Effect Size in Excel 2010 and Excel 2013
    • 1-Sample t-Test Power With G*Power Utility
    • Wilcoxon Signed-Rank Test in 8 Steps As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
    • Sign Test As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
  • 2-Independent-Sample Pooled t-Tests in Excel
    • 2-Independent-Sample Pooled t-Test in 4 Steps in Excel 2010 and Excel 2013
    • Excel Variance Tests: Levene’s, Brown-Forsythe, and F Test For 2-Sample Pooled t-Test in Excel 2010 and Excel 2013
    • Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro Wilk Tests For Two-Sample Pooled t-Test
    • Two-Independent-Sample Pooled t-Test - All Excel Calculations
    • 2- Sample Pooled t-Test – Effect Size in Excel 2010 and Excel 2013
    • 2-Sample Pooled t-Test Power With G*Power Utility
    • Mann-Whitney U Test in 12 Steps in Excel as 2-Sample Pooled t-Test Nonparametric Alternative in Excel 2010 and Excel 2013
    • 2- Sample Pooled t-Test = Single-Factor ANOVA With 2 Sample Groups
  • 2-Independent-Sample Unpooled t-Tests in Excel
    • 2-Independent-Sample Unpooled t-Test in 4 Steps in Excel 2010 and Excel 2013
    • Variance Tests: Levene’s Test, Brown-Forsythe Test, and F-Test in Excel For 2-Sample Unpooled t-Test
    • Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro-Wilk For 2-Sample Unpooled t-Test
    • 2-Sample Unpooled t-Test Excel Calculations, Formulas, and Tools
    • Effect Size for a 2-Independent-Sample Unpooled t-Test in Excel 2010 and Excel 2013
    • Test Power of a 2-Independent Sample Unpooled t-Test With G-Power Utility
  • Paired (2-Sample Dependent) t-Tests in Excel
    • Paired t-Test in 4 Steps in Excel 2010 and Excel 2013
    • Excel Normality Testing of Paired t-Test Data
    • Paired t-Test Excel Calculations, Formulas, and Tools
    • Paired t-Test – Effect Size in Excel 2010, and Excel 2013
    • Paired t-Test – Test Power With G-Power Utility
    • Wilcoxon Signed-Rank Test in 8 Steps As a Paired t-Test Alternative
    • Sign Test in Excel As A Paired t-Test Alternative
• Hypothesis Tests of Proportion in Excel
  • Hypothesis Tests of Proportion Overview (Hypothesis Testing On Binomial Data)
  • 1-Sample Hypothesis Test of Proportion in 4 Steps in Excel 2010 and Excel 2013
  • 2-Sample Pooled Hypothesis Test of Proportion in 4 Steps in Excel 2010 and Excel 2013
  • How To Build a Much More Useful Split-Tester in Excel Than Google's Website Optimizer
• Chi-Square Independence Tests in Excel
  • Chi-Square Independence Test in 7 Steps in Excel 2010 and Excel 2013
• Chi-Square Goodness-Of-Fit Tests in Excel
  • Overview of the Chi-Square Goodness-of-Fit Test
  • Chi-Square Goodness- of-Fit Test With Pre-Determined Bins Sizes in 7 Steps in Excel 2010 and Excel 2013
  • Chi-Square Goodness-Of-Fit-Normality Test in 9 Steps in Excel 2010 and Excel 2013
• F Tests in Excel
  • F-Test in 6 Steps in Excel 2010 and Excel 2013
  • Normality Testing For F Test In Excel 2010 and Excel 2013
  • Levene’s and Brown- Forsythe Tests: F-Test Alternatives in Excel
• Correlation in Excel
  • Overview of Correlation In Excel 2010 and Excel 2013
• Pearson Correlation in Excel
  • Pearson Correlation in 3 Steps in Excel 2010 and Excel 2013
  • Pearson Correlation – Calculating r Critical and p Value of r in Excel
• Spearman Correlation in Excel
  • Spearman Correlation in 6 Steps in Excel 2010 and Excel 2013
• Confidence Intervals in Excel
  • z-Based Confidence Intervals of a Population Mean in 2 Steps in Excel 2010 and Excel 2013
  • t-Based Confidence Intervals of a Population Mean in 2 Steps in Excel 2010 and Excel 2013
  • Minimum Sample Size to Limit the Size of a Confidence interval of a Population Mean
  • Confidence Interval of Population Proportion in 2 Steps in Excel 2010 and Excel 2013
  • Min Sample Size of Confidence Interval of Proportion in Excel 2010 and Excel 2013
• Simple Linear Regression in Excel
  • Overview of Simple Linear Regression in Excel 2010 and Excel 2013
  • Complete Simple Linear Regression Example in 7 Steps in Excel 2010 and Excel 2013
  • Residual Evaluation For Simple Regression in 8 Steps in Excel 2010 and Excel 2013
  • Residual Normality Tests in Excel – Kolmogorov-Smirnov Test, Anderson-Darling Test, and Shapiro-Wilk Test For Simple Linear Regression
  • Evaluation of Simple Regression Output For Excel 2010 and Excel 2013
  • All Calculations Performed By the Simple Regression Data Analysis Tool in Excel 2010 and Excel 2013
  • Prediction Interval of Simple Regression in Excel 2010 and Excel 2013
• Multiple Linear Regression in Excel
  • Basics of Multiple Regression in Excel 2010 and Excel 2013
  • Complete Multiple Linear Regression Example in 6 Steps in Excel 2010 and Excel 2013
  • Multiple Linear Regression’s Required Residual Assumptions
  • Normality Testing of Residuals in Excel 2010 and Excel 2013
  • Evaluating the Excel Output of Multiple Regression
  • Estimating the Prediction Interval of Multiple Regression in Excel
  • Regression - How To Do Conjoint Analysis Using Dummy Variable Regression in Excel
• Logistic Regression in Excel
  • Logistic Regression Overview
  • Logistic Regression in 6 Steps in Excel 2010 and Excel 2013
  • R Square For Logistic Regression Overview
  • Excel R Square Tests: Nagelkerke, Cox and Snell, and Log-Linear Ratio in Excel 2010 and Excel 2013
  • Likelihood Ratio Is Better Than Wald Statistic To Determine if the Variable Coefficients Are Significant For Excel 2010 and Excel 2013
  • Excel Classification Table: Logistic Regression’s Percentage Correct of Predicted Results in Excel 2010 and Excel 2013
  • Hosmer- Lemeshow Test in Excel – Logistic Regression Goodness-of-Fit Test in Excel 2010 and Excel 2013
• Single-Factor ANOVA in Excel
  • Overview of Single-Factor ANOVA
  • Single-Factor ANOVA in 5 Steps in Excel 2010 and Excel 2013
  • Shapiro-Wilk Normality Test in Excel For Each Single-Factor ANOVA Sample Group
  • Kruskal-Wallis Test Alternative For Single Factor ANOVA in 7 Steps in Excel 2010 and Excel 2013
  • Levene’s and Brown-Forsythe Tests in Excel For Single-Factor ANOVA Sample Group Variance Comparison
  • Single-Factor ANOVA - All Excel Calculations
  • Overview of Post-Hoc Testing For Single-Factor ANOVA
  • Tukey-Kramer Post-Hoc Test in Excel For Single-Factor ANOVA
  • Games-Howell Post-Hoc Test in Excel For Single-Factor ANOVA
  • Overview of Effect Size For Single-Factor ANOVA
  • ANOVA Effect Size Calculation Eta Squared in Excel 2010 and Excel 2013
  • ANOVA Effect Size Calculation Psi – RMSSE – in Excel 2010 and Excel 2013
  • ANOVA Effect Size Calculation Omega Squared in Excel 2010 and Excel 2013
  • Power of Single-Factor ANOVA Test Using Free Utility G*Power
  • Welch’s ANOVA Test in 8 Steps in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
  • Brown-Forsythe F-Test in 4 Steps in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
• Two-Factor ANOVA With Replication in Excel
  • Two-Factor ANOVA With Replication in 5 Steps in Excel 2010 and Excel 2013
  • Variance Tests: Levene’s and Brown-Forsythe For 2-Factor ANOVA in Excel 2010 and Excel 2013
  • Shapiro-Wilk Normality Test in Excel For 2-Factor ANOVA With Replication
  • 2-Factor ANOVA With Replication Effect Size in Excel 2010 and Excel 2013
  • Excel Post Hoc Tukey’s HSD Test For 2-Factor ANOVA With Replication
  • 2-Factor ANOVA With Replication – Test Power With G-Power Utility
  • Scheirer-Ray-Hare Test Alternative For 2-Factor ANOVA With Replication
• Two-Factor ANOVA Without Replication in Excel
  • Two-Factor ANOVA Without Replication in Excel 2010 and Excel 2013
• Randomized Block Design ANOVA in Excel
  • Randomized Block Design ANOVA in Excel 2010 and Excel 2013
• Repeated-Measures ANOVA in Excel
  • Single-Factor Repeated-Measures ANOVA in 4 Steps in Excel 2010 and Excel 2013
  • Sphericity Testing in 9 Steps For Repeated Measures ANOVA in Excel 2010 and Excel 2013
  • Effect Size For Repeated-Measures ANOVA in Excel 2010 and Excel 2013
  • Friedman Test in 3 Steps For Repeated-Measures ANOVA in Excel 2010 and Excel 2013
• ANCOVA in Excel
  • Single-Factor ANCOVA in 8 Steps in Excel 2010 and Excel 2013
• Normality Testing in Excel
  • Creating a Box Plot in 8 Steps in Excel
  • Creating a Normal Probability Plot With Adjustable Confidence Interval Bands in 9 Steps in Excel With Formulas and a Bar Chart
  • Chi-Square Goodness-of-Fit Test For Normality in 9 Steps in Excel
  • Kolmogorov-Smirnov, Anderson-Darling, and Shapiro-Wilk Normality Tests in Excel
• Nonparametric Testing in Excel
  • Mann-Whitney U Test in 12 Steps in Excel
  • Wilcoxon Signed-Rank Test in 8 Steps in Excel
  • Sign Test in Excel
  • Friedman Test in 3 Steps in Excel
  • Scheirer-Ray-Hope Test in Excel
  • Welch's ANOVA Test in 8 Steps Test in Excel
  • Brown-Forsythe F Test in 4 Steps Test in Excel
  • Levene's Test and Brown-Forsythe Variance Tests in Excel
  • Chi-Square Independence Test in 7 Steps in Excel
  • Chi-Square Goodness-of-Fit Tests in Excel
  • Chi-Square Population Variance Test in Excel
• Post Hoc Testing in Excel
  • Tukey's HSD Post Hoc Test in Excel
  • Tukey-Kramer Post Hoc Test in Excel
  • Games-Howell Post Hoc Test in Excel
• Creating Interactive Graphs of Statistical Distributions in Excel
  • Interactive Statistical Distribution Graph in Excel 2010 and Excel 2013
  • Interactive Graph of the Normal Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the Chi-Square Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the t-Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the t-Distribution’s PDF in Excel 2010 and Excel 2013
  • Interactive Graph of the t-Distribution’s CDF in Excel 2010 and Excel 2013
  • Interactive Graph of the Binomial Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the Exponential Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the Beta Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the Gamma Distribution in Excel 2010 and Excel 2013
  • Interactive Graph of the Poisson Distribution in Excel 2010 and Excel 2013
• Solving Problems With Other Distributions in Excel
  • Solving Uniform Distribution Problems in Excel 2010 and Excel 2013
  • Solving Multinomial Distribution Problems in Excel 2010 and Excel 2013
  • Solving Exponential Distribution Problems in Excel 2010 and Excel 2013
  • Solving Beta Distribution Problems in Excel 2010 and Excel 2013
  • Solving Gamma Distribution Problems in Excel 2010 and Excel 2013
  • Solving Poisson Distribution Problems in Excel 2010 and Excel 2013
• Optimization With Excel Solver
  • Maximizing Lead Generation With Excel Solver
  • Minimizing Cutting Stock Waste With Excel Solver
  • Optimal Investment Selection With Excel Solver
  • Minimizing the Total Cost of Shipping From Multiple Points To Multiple Points With Excel Solver
  • Knapsack Loading Problem in Excel Solver – Optimizing the Loading of a Limited Compartment
  • Optimizing a Bond Portfolio With Excel Solver
  • Travelling Salesman Problem in Excel Solver – Finding the Shortest Path To Reach All Customers
• Chi-Square Population Variance Test in Excel
  • Overview of the Chi-Square Population Variance Test in Excel 2010 and Excel 2013
• Analyzing Data With Pivot Tables
  • Pivot Tables - How To Set Up a Pivot Table Query Correctly Every Time
  • Pivot Charts - One Easy Visual Presentation That Will Double The Effect of Pivot Tables
• SEO Functions in Excel
  • Top 10 Excel SEO Functions - You'll Like These
• Time Series Analysis in Excel
  • Forecasting With Exponential Smoothing in Excel
  • Forecasting With the Weighted Moving Average in Excel
  • Forecasting With the Simple Moving Average in Excel
• VLOOKUP
  • VLOOKUP - Just Like Looking Up a Number in a Telephone Book
  • VLOOKUP To Look Up a Discount in a Distant Database

 

Technorati Tags: anova,statistics,excel,excel 2010,excel 2013,two-factor anova,two-way anova,two factor anova,two way anova