Wednesday, April 28, 2010

Logistic Regression - How To Predict If a Prospect Will Buy Using Logistic Regression in Excel

Logistic Regression

Analysis in Excel

For Marketing



Wouldn’t it be great if there was a more accurate way to predict whether your prospect will buy rather than just taking an educated guess? Well, there is…if you have enough data on your previous prospects. The tool that makes this possible is called Logistic Regression and can be easily implemented in Excel.




Customer Quality Scores Are Created With Logistic Regression


Marketers use Logistic Regression to rank their prospects with a quality score which indicates that prospect’s likelihood to buy. The more data you’ve collected from previous prospects, the more accurately you’ll be able to use Logistic Regression in Excel to calculate your new prospect’s probability of purchasing.


Here is a video which will show you how to perform Logistic Regression in Excel and why it works. The example that will be presented in the video will also be covered below in the article:




Step-By-Step Video Showing How To Predict if a Prospect Will Buy Using Logistic Regression in Excel:
(Is Your Sound Turned On?)




What is Logistic Regression?


Logistic Regression calculates the probability of the event occurring, such as the purchase of a product. In general, the thing being predicted in a Regression equation is represented by the dependent variable or output variable and is usually labeled as the Y variable in the Regression equation. In the case of Logistic Regression, this “Y” is binary. In other words, the output or dependent variable can only take the values of 1 or 0. The predicted event either occurs or it doesn’t occur – your prospect either will buy or won’t buy. Occasionally this type of output variable also referred to as a Dummy Dependent Variable.




An Example of Logistic Regression In Action


Here is a marketing example showing how Logistic Regression works. The embedded video walks through this example in Excel as well:


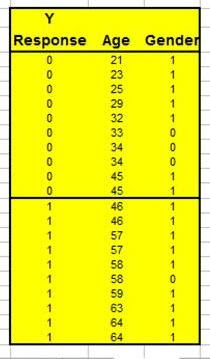
Suppose that you have collected three pieces of data on each of your previous prospects. The data you have collected on each prospect was:


1) The prospect’s age
2) The prospect’s gender (1 = Male and 0 = Female)
3) Whether the prospect purchased or not (Did purchase Y = 1, Did not purchase, Y = 0).
regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel






Create the Predictive Equation


With the above data, you could create a predictive equation that would calculate a new prospect’s probability of purchasing by inputting this new prospect’s age and gender. This predictive equation will be in the form of:


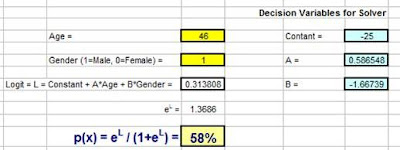
P(X) = eL/ (1+eL)


P(X) represents the possibility of event X occurring.




The Logit


Event X is a purchase. In other words, P(X) is the probability that Y = 1.


P(X) has only one variable. That is L, which is called the Logit.


The Logit, L = Constant + A * Age + B * Gender


L, the Logit, has 3 variables: Constant, A, and B. They must be known before P(X) can be calculated. Those 3 variables can be found in Excel by using the Excel Solver. The Excel Solver will find the optimal combination of those 3 variables that causes the resulting P(X) to most accurately predict whether Y = 1 or 0 for all previous prospects.




regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel
Click On Image To See Larger Version



Calculating the Logit Variables - A, B, and Constant


Here’s how the most optimal set of Logit variables (Constant, A, and B) are found in Excel:


Using Excel, each recorded prospect has the following calculation performed:


P(X)Y * [ 1 - P(X) ](1-Y)


The Y refers to Y = 1 if the prospect bought and Y = 0 if the prospect didn’t buy.


The P(X) is the probability of purchase that will be calculated using the equation listed above. In Excel, the P(X) calculation is initially performed by the Excel Solver using Logit variables (Constant, A, and B) which are not optimal. The Excel Solver will then continuously try new combinations of these variables until the optimal P(X) is found.

Optimizing the Logit Variables in the Excel Solver


Here’s how the Excel Solver knows when it has found the correct combinations of these 3 variables so that the resulting P(X) equation most accurately predicts whether Y = 1 or 0:


The equation P(X )Y * [ 1 - P(X) ](1-Y) is maximized when P(X) is most accurate. It approaches it highest value (1) when Y = 1 and P(X) approaches 1. It also approaches its highest value (1) when Y = 0 and P(X) approaches 0. When Y = 1 and P(X) = 1, that is a 100% correct prediction by P(X) that Y = 1. When Y = 0 and P(X) = 0, that is a 100% correct prediction by P(X) that Y = 0.


Each prospect has a separate P(X )Y * [ 1 - P(X) ](1-Y) value calculated for him or her.


The sum of each P(X )Y * [ 1 - P(X) ](1-Y) calculation for all prospects is taken.


The only variables that exist when calculating P(X )Y * [ 1 - P(X) ](1-Y) are Y and the variables of P(X), which are Constant, A, and B. Use the Excel Solver, these variable are adjusted until their values maximize the sum of all P(X )Y * [ 1 - P(X) ](1-Y).


regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel




The Final, Most Accurate Predictive Equation


When the sum of P(X )Y * [ 1 - P(X) ](1-Y) is maximized, then the final resulting P(X) equation is as accurate as possible at predicting whether Y will be 1 or 0.


regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel
Click On Image To See Larger Version



The Excel Solver Dialogue Box
regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel


Stated another way, we now have a predictive equation P(X ) which uses the optimal combination of Constant, A, and B which most accurately calculates the probability that Y = 1 given a prospect’s age and gender.


The embedded video provides a clear picture of all of this in action in Excel.


The use of the Excel Solver does require some hand-tweeking to ensure that the most accurate answer is obtained. The video shows an example of this. Ultimately what the Solver is doing is adjusting variables Constant, A, and B to maximize the sum of the column of


P(X )Y * [ 1 - P(X) ](1-Y) equations. The answer obtained by the Solver should maximize that sum and provide realistic answers for the probabilities of each prospect, including the new one.






You'll Have To Tweek the Constraints in the Excel Solver


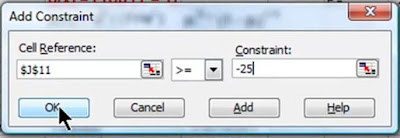
You’ll probably find that you have to experiment by applying constraints to the variables that Solver is adjusting in order to maximize the target sum. The variables that Solver adjusts are called Decision Variables. Solver allows you to create constraints on the value of any Decision Variable.




Adding a Constraint to the Solver
regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel




regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel




In the video, you will be able to watch how a Decision Variable is constrained to make the final answer more accurate. The Decision Variable called Constant was constrained to always remain above -25 during the Solver analysis. This resulted in the most accurate and realistic maximization of the sum of the P(X )Y * [ 1 - P(X) ](1-Y) equations.




Conclusion - Incredible Predictor but Not the Simplest Analysis


Logistic Regression is not the simplest type of analysis to understand or perform. Hopefully this article and video have provided a much clearer picture for you.

 regression, logistic regression, logit regression, logit, regression model, logit model, logistic regression spss, logistic regression models, statistical analysis in excel





If you have any comments, questions, suggestions regarding the use of Logistic Regression, your input is welcome and appreciated.



If You Like This, Then Share It...
Dig this Stumble upon Delicious Technorati Reddit Buzz it Twitthis

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at
Labels: , , , , , , , ,

15 comments:

  1. AnonymousFebruary 13, 2012 at 8:23 AM

    sorry for the duplicate comment

    ReplyDelete
  2. AnonymousFebruary 23, 2012 at 5:18 PM

    Thanks so much for such a helpful tutorial!

    ReplyDelete
  3. Mark HarmonFebruary 24, 2012 at 12:40 PM

    Why Thanks! Really great to hear that you found it useful :>D

    ReplyDelete
    Replies
    1. AnonymousMarch 1, 2012 at 1:11 AM

      Can you please explain how you determined >=-25 constraint in your example?

      Many Thanks!

      Delete
  4. Matt MarshallDecember 28, 2012 at 10:36 AM

    Is there any way to calculate dispersion statistics, too? Thanks!

    ReplyDelete
  5. vé máy bay từ canada về việt namSeptember 15, 2021 at 8:22 PM

    Mua vé tại Aivivu, tham khảo

    mua ve may bay di my

    vé máy bay từ mỹ về vn

    ve may bay tư duc ve viet nam

    chuyến bay từ nga về việt nam

    chuyến bay từ anh về việt nam

    chuyến bay từ Paris về Hà Nội

    các khách sạn cách ly ở quảng ninh

    chuyến bay chuyên gia trung quốc

    ReplyDelete
  6. JacobHarmanMay 1, 2022 at 4:41 PM

    This comment has been removed by the author.

    ReplyDelete
  7. NathanPassDecember 11, 2022 at 5:05 AM

    Hello! Sometimes students are given the task to find the adverb in text. This can take a lot of time and not all students are able to accurately find adverbs in their text. But what if you want to complete such a task perfectly? Then use our adverb checker! This is the best way that will not let you down!

    ReplyDelete
  8. DarenTillDecember 14, 2022 at 6:45 AM

    How to change to active voice in text? Everything is very simple! All you need to do is start using a specialized tool, thanks to which you can do it quickly and without problems! This tool specializes in active voice, and can easily convert passive voice to active voice within text.

    ReplyDelete
  9. NathanPassDecember 17, 2022 at 5:40 AM

    Hello! Increasingly, students are looking on the Internet for passive voice misuse check app so as not to waste time correcting the passive voice themselves. And I want to recommend you a tool that you can test right now! This assistant is absolutely free and will help you fully check your text and convert your passive voice!

    ReplyDelete
  10. hrdnmxdvlpFebruary 14, 2023 at 4:37 PM

    If you are a company owner and want to make the resource management process easier, then you should visit our website, because there we talk about such an opportunity. We offer you to read an article about compare microsoft dynamics crm and salesforce, because it is one of the most importante questions.

    ReplyDelete
  11. JohnsonMarch 7, 2023 at 1:51 AM

    If you want information about Excel, then you will get the best information from this post. You will get a lot of benefit from this information to move forward in your career. My friend told me about run-on sentence checker tool yesterday. He also taught me how to use that tool. Using this tool is very easy. You can also improve your English with this tool.

    ReplyDelete
  12. LeoMarch 16, 2023 at 4:02 AM

    If you are a professional speechwriter, you spend countless hours editing your speech drafts. Worse still, hiring a professional editor doesn’t come cheap. With the help of our sentence part identifier tool, you can save both time and money that would have otherwise gone into hiring a professional editor.

    ReplyDelete
  13. R H Construction USA INCMarch 17, 2023 at 7:40 AM

    Through this post I am going to itroduce you guys all about the professional part of speech finder for excellent writing. No doubt it has amazing tool for improving writing. It is good wat to identifying the different part of speech and use them in correctly. I am sure this service will sucessfully gain your trust in first time. The parts of speech checker tool are very helpful for in these days.

    ReplyDelete
  14. John FeiApril 16, 2024 at 2:08 AM

    The Attract Group's post on finding developers for startups is an invaluable resource. It offers practical, clear advice, highlighting the importance of aligning with a developer who shares your startup's vision. The emphasis on cultural fit and technical expertise is spot-on, equipping entrepreneurs with the right tools to build a solid tech foundation.

    ReplyDelete

Subscribe to: Post Comments (Atom)