Friday, May 30, 2014

Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro Wilk Tests For Two-Sample Pooled t-Test

This is one of the following eight articles on 2-Independent-Sample Pooled t-Tests in Excel

2-Independent-Sample Pooled t-Test in 4 Steps in Excel 2010 and Excel 2013

Excel Variance Tests: Levene’s, Brown-Forsythe, and F Test For 2-Sample Pooled t-Test in Excel 2010 and Excel 2013

Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro Wilk Tests For Two-Sample Pooled t-Test

Two-Independent-Sample Pooled t-Test - All Excel Calculations

2-Sample Pooled t-Test – Effect Size in Excel 2010 and Excel 2013

2-Sample Pooled t-Test Power With G*Power Utility

Mann-Whitney U Test in 12 Steps in Excel as 2-Sample Pooled t-Test Nonparametric Alternative in Excel 2010 and Excel 2013

2- Sample Pooled t-Test = Single-Factor ANOVA With 2 Sample Groups

 

Excel Normality Tests

Kolmogorov-Smirnov,

Anderson-Darling, and

Shapiro Wilk Tests For

Two-Sample Pooled t-Test

The following five normality tests will be performed on the sample data here:

An Excel histogram of the sample data will be created.

A normal probability plot of the sample data will be created in Excel.

The Kolmogorov-Smirnov test for normality of the sample data will be performed in Excel.

The Anderson-Darling test for normality of the sample data will be performed in Excel.

The Shapiro-Wilk test for normality of the sample data will be performed in Excel.

The quickest way to evaluate normality of a sample is to construct an Excel histogram from the sample data.

 

Histogram in Excel

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

To create this histogram in Excel, fill in the Excel Histogram dialogue box as follows:

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

To create this histogram in Excel, fill in the Excel Histogram dialogue box as follows:

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

Both sample groups appear to be distributed reasonably closely to the bell-shaped normal distribution. It should be noted that bin size in an Excel histogram is manually set by the user. This arbitrary setting of the bin sizes can has a significant influence on the shape of the histogram’s output. Different bin sizes could result in an output that would not appear bell-shaped at all. What is actually set by the user in an Excel histogram is the upper boundary of each bin.

 

Normal Probability Plot in Excel

Another way to graphically evaluate normality of each data sample is to create a normal probability plot for each sample group. This can be implemented in Excel and appears as follows:

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

Normal probability plots for both sample groups show that the data appears to be very close to being normally distributed. The actual sample data (red) matches very closely the data values of the sample were perfectly normally distributed (blue) and never goes beyond the 95 percent confidence interval boundaries (green).

 

Kolmogorov-Smirnov Test For

Normality in Excel

The Kolmogorov-Smirnov Test is a hypothesis test that is widely used to determine whether a data sample is normally distributed. The Kolmogorov-Smirnov Test calculates the distance between the Cumulative Distribution Function (CDF) of each data point and what the CDF of that data point would be if the sample were perfectly normally distributed. The Null Hypothesis of the Kolmogorov-Smirnov Test states that the distribution of actual data points matches the distribution that is being tested. In this case the data sample is being compared to the normal distribution.

The largest distance between the CDF of any data point and its expected CDF is compared to Kolmogorov-Smirnov Critical Value for a specific sample size and Alpha. If this largest distance exceeds the Critical Value, the Null Hypothesis is rejected and the data sample is determined to have a different distribution than the tested distribution. If the largest distance does not exceed the Critical Value, we cannot reject the Null Hypothesis, which states that the sample has the same distribution as the tested distribution.

F(Xk) = CDF(Xk) for normal distribution

F(Xk) = NORM.DIST(Xk, Sample Mean, Sample Stan. Dev., TRUE)

 

Variable 1 - Brand A Battery Lifetimes

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

0.0885 = Max Difference Between Actual and Expected CDF

16 = n = Number of Data Points

0.05 = α

 

Variable 2 - Brand B Battery Lifetimes

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

0.1007 = Max Difference Between Actual and Expected CDF

17 = n = Number of Data Points

0.05 = α

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

The Null Hypothesis Stating That the Data Are Normally Distributed Cannot Be Rejected

The Null Hypothesis for the Kolmogorov-Smirnov Test for Normality, which states that the sample data are normally distributed, is rejected only if the maximum difference between the expected and actual CDF of any of the data points exceed the Critical Value for the given n and α. That is not the case here.

The Max Difference Between the Actual and Expected CDF for Variable 1 (0.0885) and for Variable 2 (0.1007) are significantly less than the Kolmogorov-Smirnov Critical Value for n = 20 (0.29) and for n = 15 (0.34) at α = 0.05 so the Null Hypotheses of the Kolmogorov-Smirnov Test of each of the two sample groups is accepted.

 

Anderson-Darling Test For

Normality in Excel

The Anderson-Darling Test is a hypothesis test that is widely used to determine whether a data sample is normally distributed. The Anderson-Darling Test calculates a test statistic based upon the actual value of each data point and the Cumulative Distribution Function (CDF) of each data point if the sample were perfectly normally distributed.

The Anderson-Darling Test is considered to be slightly more powerful than the Kolmogorov-Smirnov test for the following two reasons:

The Kolmogorov-Smirnov test is distribution-free. i.e., its critical values are the same for all distributions tested. The Anderson-darling tests requires critical values calculated for each tested distribution and is therefore more sensitive to the specific distribution.

The Anderson-Darling test gives more weight to values in the outer tails than the Kolmogorov-Smirnov test. The K-S test is less sensitive to aberration in outer values than the A-D test.

If the test statistic exceeds the Anderson-Darling Critical Value for a given Alpha, the Null Hypothesis is rejected and the data sample is determined to have a different distribution than the tested distribution. If the test statistic does not exceed the Critical Value, we cannot reject the Null Hypothesis, which states that the sample has the same distribution as the tested distribution.

F(Xk) = CDF(Xk) for normal distribution

F(Xk) = NORM.DIST(Xk, Sample Mean, Sample Stan. Dev., TRUE)

Variable 1 – Brand A Battery Lifetimes

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

Adjusted Test Statistic A* = 0.174

 

Variable 2 - Brand B Battery Lifetimes

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

Adjusted Test Statistic A* = 0.227

Reject the Null Hypothesis of the Anderson-Darling Test which states that the data are normally distributed if any the following are true:

A* > 0.576 When Level of Significance (α) = 0.15

A* > 0.656 When Level of Significance (α) = 0.10

A* > 0.787 When Level of Significance (α) = 0.05

A* > 1.092 When Level of Significance (α) = 0.01

The Null Hypothesis Stating That the Data Are Normally Distributed Cannot Be Rejected

The Null Hypothesis for the Anderson-Darling Test for Normality, which states that the sample data are normally distributed, is rejected if the Adjusted Test Statistic (A*) exceeds the Critical Value for the given n and α.

The Adjusted Test Statistic (A*) for Variable 1 (0.174) and for Variable 2 (0.227) are significantly less than the Anderson-Darling Critical Value for α = 0.05 so the Null Hypotheses of the Anderson-Darling Test for each of the two sample groups is accepted.

 

Shapiro-Wilk Test For Normality in

Excel

The Shapiro-Wilk Test is a hypothesis test that is widely used to determine whether a data sample is normally distributed. A test statistic W is calculated. If this test statistic is less than a critical value of W for a given level of significance (alpha) and sample size, the Null Hypothesis which states that the sample is normally distributed is rejected.

The Shapiro-Wilk Test is a robust normality test and is widely-used because of its slightly superior performance against other normality tests, especially with small sample sizes. Superior performance means that it correctly rejects the Null Hypothesis that the data are not normally distributed a slightly higher percentage of times than most other normality tests, particularly at small sample sizes.

The Shapiro-Wilk normality test is generally regarded as being slightly more powerful than the Anderson-Darling normality test, which in turn is regarded as being slightly more powerful than the Kolmogorov-Smirnov normality test.

Variable 1 – Brand A Battery Life

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

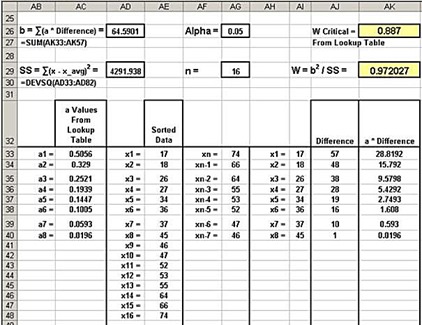
0.972027 = Test Statistic W

0.887 = W Critical for the following n and Alpha

16 = n = Number of Data Points

0.05 = α

The Null Hypothesis Stating That the Data Are Normally Distributed Cannot Be Rejected

Test Statistic W (0. 972027) is larger than W Critical 0.887. The Null Hypothesis therefore cannot be rejected. There is not enough evidence to state that the data are not normally distributed with a confidence level of 95 percent.

Variable 2 – Brand B Battery Life

normality test,kolmogorov, anderson-darling,shapiro-wilk,t-test,t test,excel,excel 2010,excel 2013,statistics (Click On Image To See a Larger Version)

0.971481 = Test Statistic W

0.892 = W Critical for the following n and Alpha

17 = n = Number of Data Points

0.05 = α

The Null Hypothesis Stating That the Data Are Normally Distributed Cannot Be Rejected

Test Statistic W (0. 971481) is larger than W Critical 0.892. The Null Hypothesis therefore cannot be rejected. There is not enough evidence to state that the data are not normally distributed with a confidence level of 95 percent.

 

Correctable Reasons That Normal

Data Can Appear Non-Normal

If a normality test indicates that data are not normally distributed, it is a good idea to do a quick evaluation of whether any of the following factors have caused normally-distributed data to appear to be non-normally-distributed:

 

1) Outliers

– Too many outliers can easily skew normally-distributed data. An outlier can oftwenty be removed if a specific cause of its extreme value can be identified. Some outliers are expected in normally-distributed data.

 

2) Data Has Been Affected by More Than One Process

– Variations to a process such as shift changes or operator changes can change the distribution of data. Multiple modal values in the data are common indicators that this might be occurring. The effects of different inputs must be identified and eliminated from the data.

 

3) Not Enough Data

– Normally-distributed data will often not assume the appearance of normality until at least 25 data points have been sampled.

 

4) Measuring Devices Have Poor Resolution

– Sometimes (but not always) this problem can be solved by using a larger sample size.

 

5) Data Approaching Zero or a Natural Limit

– If a large number of data values approach a limit such as zero, calculations using very small values might skew computations of important values such as the mean. A simple solution might be to raise all the values by a certain amount.

 

6) Only a Subset of a Process’ Output Is Being Analyzed

– If only a subset of data from an entire process is being used, a representative sample in not being collected. Normally-distributed results would not appear normally distributed if a representative sample of the entire process is not collected.

 

When Data Are Not Normally

Distributed

When normality of data cannot be confirmed for a small sample, it is necessary to substitute a nonparametric test for a t-Test. Nonparametric tests do not have the same normality requirement that the t-Test does. The most common nonparametric test that can be substituted for the two-independent-sample t-Test when data normality cannot be confirmed is the Mann-Whitney U Test.

The Mann-Whitney U Test is performed on the data in this example in a blog article following this one. Nonparametric tests are generally less powerful (less able to detect a difference) than parametric tests. The parametric two-independent sample, one-tailed t-Test performed here does detect a difference at alpha = 0.05. the nonparametric Mann-Whitney U test conducted at the end of this section on the same data did not detect a difference at alpha = 0.05.

 

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at

11 comments:

  1. UnknownJuly 11, 2018 at 5:30 AM

    Well done! It is so well written and interactive. Keep writing such brilliant piece of work. Glad i came across this post. Last night even i saw similar wonderful R Programming tutorial on youtube so you can check that too for more detailed knowledge on R Programming.https://www.youtube.com/watch?v=rgFVq_Q6VF0

    ReplyDelete
    Replies
    1. AnonymousDecember 7, 2022 at 8:51 AM

      I'm a student. I work part-time at Euristiq. I recommend you to visit our site.
      Euristiq is committed to helping customers achieve greater efficiency and more income. They are currently working on projects for clients throughout the world. They are based in Lviv, Ukraine.
      An iot cloud platform can also help you make sense of all of the data you collect. The best platforms can help you to get the most out of your data by leveraging analytics and artificial intelligence. Some of the best IoT platforms are able to process live patient vitals and provide recommendations on how to improve your patient experience.

      Delete
  2. UnknownJuly 17, 2018 at 1:55 AM

    What a fantastic read on Data Science. This has helped me understand a lot in Data Science course. Please keep sharing similar write ups on Data Science. Guys if you are keen to know more on Data Science, must check this wonderful Data Science tutorial and i'm sure you will enjoy learning on Data Science training.:-https://www.youtube.com/watch?v=gXb9ZKwx29U&t=237s

    ReplyDelete
  3. JackStoneJanuary 27, 2022 at 12:21 AM

    Thank God my parents didn’t force me to choose statistics as my subject even though they wanted me to but I knew I can never comprehend it. I’m happy with my literature subject where I read, write, and sometimes even get to Project Management Assignment Help when needed. So; I’m living a stress-free life.

    ReplyDelete
    Replies
    1. VitalikPaliyDecember 1, 2024 at 2:40 PM

      While these services can be helpful, they should be used ethically, as relying on them excessively might hinder personal academic growth. Always review the essay thoroughly and use it as a guide or reference to better understand the subject matter. Using a pay for essays Essay Shark service can be a convenient option for students facing tight deadlines or struggling with complex topics. These platforms often provide access to skilled writers who can craft custom essays tailored to specific requirements. However, it's essential to approach such services with caution. Ensure the provider is reputable, offers plagiarism-free content, and respects deadlines.

      Delete
  4. Łukasz KowalczykJuly 11, 2022 at 12:14 PM

    Hi all! This post is really awesome, so thanks for sharing this helpful information on this site! What about me, I'm currently working as a writer for a huge education company. If you need help writing custom assignments, visit the Professional Writing Agency website custom essay writing service link where you can buy correct essays. And we can help with any learning problem you want!!!

    ReplyDelete
  5. AnthonyRileyDecember 7, 2022 at 5:22 AM

    This comment has been removed by the author.

    ReplyDelete
  6. AnonymousDecember 7, 2022 at 5:34 AM

    Tutors are hired based on their knowledge, experience, and personality. To ensure that the company provides quality service, does an internal check of applicants. In addition, tutors are required to pass an English proficiency test.
    Whether you are a college student who needs to pay for homework https://domyhomeworkabc.com/ , or a parent who needs to pay for your child's schoolwork, there are several websites where you can find a professional who will complete your assignment.

    ReplyDelete
  7. AnthonyRileyDecember 24, 2022 at 1:50 PM

    One thing you should do before you buy a dissertation dissertation-writer.org is check out the website's reviews. This will give you an idea of what kind of customers the site has. Often, the customer testimonials will be about the quality of the services they received. Additionally, you should read the list of awards the company has won.

    ReplyDelete
  8. AnonymousDecember 24, 2022 at 1:53 PM

    Fortunately, there are several websites buyessaypaper.org out there that will help you to find a reputable service to buy an essay from. Make sure to do your homework and take the time to read through the site's reviews. It's worth it in the long run to find a reliable writing service that will do all of the things you need in your assignment. By doing so, you'll be able to spend more time studying and less time worrying about your assignments.

    ReplyDelete
  9. jamesbarnsJuly 25, 2023 at 2:16 AM

    The excellent study guides, practice questions and answers and Splunk SPLK-1005 pdf Dumps dumps offered by DumpsCollection are your real strength to take the test with confidence and pass it without facing any difficulty.

    ReplyDelete

Subscribe to: Post Comments (Atom)