Thursday, May 29, 2014

Shapiro-Wilk Normality Test in Excel For Each Single-Factor ANOVA Sample Group

This is one of the following sixteen articles on Single-Factor ANOVA in Excel

Overview of Single-Factor ANOVA

Single-Factor ANOVA in 5 Steps in Excel 2010 and Excel 2013

Shapiro-Wilk Normality Test in Excel For Each Single-Factor ANOVA Sample Group

Kruskal-Wallis Test Alternative For Single Factor ANOVA in 7 Steps in Excel 2010 and Excel 2013

Levene’s and Brown-Forsythe Tests in Excel For Single-Factor ANOVA Sample Group Variance Comparison

Single-Factor ANOVA - All Excel Calculations

Overview of Post-Hoc Testing For Single-Factor ANOVA

Tukey-Kramer Post-Hoc Test in Excel For Single-Factor ANOVA

Games-Howell Post-Hoc Test in Excel For Single-Factor ANOVA

Overview of Effect Size For Single-Factor ANOVA

ANOVA Effect Size Calculation Eta Squared in Excel 2010 and Excel 2013

ANOVA Effect Size Calculation Psi – RMSSE – in Excel 2010 and Excel 2013

ANOVA Effect Size Calculation Omega Squared in Excel 2010 and Excel 2013

Power of Single-Factor ANOVA Test Using Free Utility G*Power

Welch’s ANOVA Test in 8 Steps in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar

Brown-Forsythe F-Test in 4 Steps in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar

 

Shapiro-Wilk Test For

Normality in Excel

There are a number of normality test that can be performed on each group’s data. The normality test that is preferred because it is considered to be more powerful (accurate) than the others, particularly with smaller sample sizes is the Shapiro-Wilk test.

The Shapiro-Wilk Test is a hypothesis test that is widely used to determine whether a data sample is normally-distributed. A test statistic W is calculated. If this test statistic is less than a critical value of W for a given level of significance (alpha) and sample size, the Null Hypothesis which states that the sample is normally-distributed is rejected.

The Shapiro-Wilk Test is a robust normality test and is widely-used because of its slightly superior performance against other normality tests, especially with small sample sizes. Superior performance means that it correctly rejects the Null Hypothesis that the data are not normally-distributed a slightly higher percentage of times than most other normality tests, particularly at small sample sizes.

The Shapiro-Wilk normality test is generally regarded as being slightly more powerful than the Anderson-Darling normality test, which in turn is regarded as being slightly more powerful than the Kolmogorov-Smirnov normality test.

 

Shapiro-Wilk Normality Test of

Group 1 Test Scores

shapiro,normality test,excel, anova,excel 2010,excel 2013,statistics,single-factor anova,one-way anova (Click Image To See a Larger Version)

0.964927 = Test Statistic W

0.911 = W Critical for the following n and Alpha

22 = n = Number of Data Points

0.05 = α

The Null Hypothesis Stating That the Data Are Normally-Distributed Cannot Be Rejected

Test Statistic W (0.964927) is larger than W Critical 0.911. The Null Hypothesis therefore cannot be rejected. There is not enough evidence to state that Group 1 data are not normally-distributed with a confidence level of 95 percent.

 

Shapiro-Wilk Normality Test of

Group 2 Test Scores

shapiro,normality test,excel, anova,excel 2010,excel 2013,statistics,single-factor anova,one-way anova
(Click Image To See a Larger Version)

0.966950 = Test Statistic W

0.914 = W Critical for the following n and Alpha

23 = n = Number of Data Points

0.05 = α

The Null Hypothesis Stating That the Data Are Normally-distributed Cannot Be Rejected

Test Statistic W (0.964927) is larger than W Critical 0.911. The Null Hypothesis therefore cannot be rejected. There is not enough evidence to state that Group 2 data are not normally-distributed with a confidence level of 95 percent.

Shapiro-Wilk Normality Test of Group 3 Test Scores

shapiro,normality test,excel, anova,excel 2010,excel 2013,statistics,single-factor anova,one-way anova
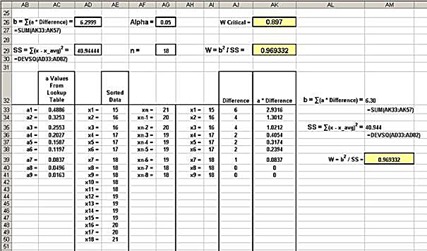
(Click Image To See a Larger Version)

0.969332 = Test Statistic W

0.897 = W Critical for the following n and Alpha

18 = n = Number of Data Points

0.05 = α

The Null Hypothesis Stating That the Data Are Normally-distributed Cannot Be Rejected

Test Statistic W (0.969332) is larger than W Critical 0.897. The Null Hypothesis therefore cannot be rejected. There is not enough evidence to state that Group 3 data are not normally-distributed with a confidence level of 95 percent.

 

Correctable Reasons Why Normal

Data Can Appear Non-Normal

If a normality test indicates that data are not normally-distributed, it is a good idea to do a quick evaluation of whether any of the following factors have caused normally-distributed data to appear to be non-normally-distributed:

 

1) Outliers

– Too many outliers can easily skew normally-distributed data. An outlier can often be removed if a specific cause of its extreme value can be identified. Some outliers are expected in normally-distributed data.

 

2) Data Has Been Affected by More Than One Process

– Variations to a process such as shift changes or operator changes can change the distribution of data. Multiple modal values in the data are common indicators that this might be occurring. The effects of different inputs must be identified and eliminated from the data.

 

3) Not Enough Data

– Normally-distributed data will often not assume the appearance of normality until at least 25 data points have been sampled.

 

4) Measuring Devices Have Poor Resolution

– Sometimes (but not always) this problem can be solved by using a larger sample size.

 

5) Data Approaching Zero or a Natural Limit

– If a large number of data values approach a limit such as zero, calculations using very small values might skew computations of important values such as the mean. A simple solution might be to raise all the values by a certain amount.

 

6) Only a Subset of a Process’ Output Is Being Analyzed

– If only a subset of data from an entire process is being used, a representative sample in not being collected. Normally-distributed results would not appear normally-distributed if a representative sample of the entire process is not collected.

 

Nonparametric Alternatives To

Single-Factor ANOVA For Non-

Normal Data

When groups cannot be shown to all have normally-distributed data, a nonparametric test called the Kruskal-Wallis test should be performed instead of Single-Factor ANOVA. The Kruskal-Wallis Normality test will be performed on this example’s sample data in the next blog article.

 

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

 

Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)