This is one of the following four articles on the Binomial Distribution in Excel
Overview of the Binomial Distribution in Excel 2010 and Excel 2013
Solving Problems With the Binomial Distribution in Excel 2010 and Excel 2013
Normal Approximation of the Binomial Distribution in Excel 2010 and Excel 2013
Distributions Related to the Binomial Distribution
Normal Approximation of
the Binomial
Distribution in Excel
For certain values of n and p, the binomial distribution can be closely approximated by the normal distribution. This allows for quick and easy normal-distribution-based hypothesis testing and confidence interval creation for sample data that are binomially distributed.
There are several different guidelines specifying the ranges of n and p that are appropriate for approximation of the binomial distribution with the normal distribution. The normal approximation of the binomial distribution works when n is large enough and p and q are not close to zero.
The most widely-applied guideline is the following: np > 5 and nq > 5. Other sources state that normal approximation of the binomial distribution is appropriate only when np > 10 and nq > 10. this manual will utilize the first rule-of-thumb mentioned here, i.e., np > 5 and nq > 5.
Each unique binomial distribution is completely described by its two parameters n (number of trials) and p probability of success in each trial). Each unique normal distribution is completely described by its two parameters μ (mean) and σ (standard deviation).
For the appropriate ranges of n and p, the normal distribution approximates the binomial distribution by substituting np for μ and ![]() for σ.
for σ.
The Excel formula to calculate the PDF for the normal distribution at X is given as follows:
NORM.DIST(X,μ,σ,FALSE)
The Excel formula to calculate the PDF for the binomial distribution at X is given as follows:
BINOM.DIST(X,n,p,FALSE)
This is closely approximated for the appropriate ranges of n and p with the normal distribution in Excel as follows:
NORM.DIST(X,np,SQRT(npq),FALSE)
The CDF is calculated by substituting TRUE for FALSE in the Excel formula.
Following is a comparison of the normal approximation of the binomial distribution as n increases. Both the PDF and the CDF for binomial distribution and the normal distribution’s approximation are calculated. The PDF is very close even at low values of n. The CDF remains significantly different in this case until n has reached 80.
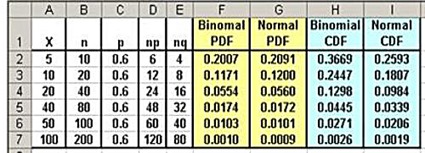
(Click On Image To See a Larger Version)
Continuity Correction
The continuity correction is an addition of 0.5 to the normal CDF’s X value. This makes the normal CDF more closely approximate the binomial CDF. The continuity correction of 0.5 is added to X to calculate the normal CDF in the following Excel chart. It can be seen that the normal CDF is a significantly better approximation of the binomial CDF with the continuity correction than without it.
A continuity correction factor of +0.5 is applied to the X value when using a continuous function (the normal distribution) to approximate the CDF of a discrete function (the binomial distribution).
The binomial’s CDF is calculated in Excel by this formula:
BINOM.DIST(X,n,p,TRUE)
The normal approximation would now be calculated by the following formula with the continuity correction of 0.5 added to X
NORM.DIST(X+0.5,np,SQRT(npq),TRUE)

(Click On Image To See a Larger Version)
The continuity correction is much less important than it used to be. Exact values of the binomial’s PDF and CDF can be calculated with specific Excel formulas. The normal approximation of the binomial distribution allows for quick and easy normal-distribution-based analysis tools such as hypothesis testing and confidence intervals to be applied to binomially-distributed data. The continuity correction is not used when performing these techniques.
Excel Master Series Blog Directory
Click Here To See a List Of All
Statistical Topics And Articles In
This Blog
You Will Become an Excel Statistical Master!






Before you start gambling for real money aici you should take the time to read the rules enough times to know the game inside and out. Without a solid understanding of the basics, you won’t be able properly grasp advanced strategy.
ReplyDeleteI enjoy reading this post. This is so informative. lanai screening Port Charlotte, FL
ReplyDelete