Excel Master Series Blog: Probability in Excel

Saturday, April 4, 2015

Probability in Excel

Probability Overview

The probability of an event occurring is expressed on a linear scale between 0 and 1. A probability of 0 indicates that there is 0-percent chance of the event occurring and a probability of 1 indicates that there is a 100-percent chance of the event occurring.

Experiment or Trial

A process that produces a single outcome that is uncertain. An example of an experiment would be the single roll of one dice.

Outcome

Any possible result of a single trial or experiment. An outcome of a random selection of a single card from a deck of cards has 52 possible outcomes. The sum of the probabilities of all possible outcomes equals 1. The sum of the probability of all possible outcomes can be expressed as follows:

If each possible outcome has the same probability of occurring as any other outcome, the probability of each and every outcome, P(E_i), can be calculated as follows:

P(E_i) = 1 / (number of all possible outcomes)

The probability of randomly selecting any specific card from a 52-card deck is equal to 1/52 = 0.0192. This means that there is a 1.92-percent chance of randomly drawing a specific card such as a Queen of Hearts.

P(E_i) = 1 / (number of all possible outcomes)

P(Queen of Hearts) = 1/52 = 0.0192 = 1.92%

A generalization of concept occurs when objects are distributed according to the universal distribution. All of the possible outcomes contain the same number of objects if a group of objects is universally distributed. Suits of cards in a regular deck are universally distributed because a deck contains 13 diamonds, 13 hearts, 13 clovers, and 13 spades.

P(E_i for universally distributed objects) = (number of objects in each outcome)/(total number of objects)

For example, the probability of randomly selecting a card of any specific suit, say queens, would be the following:

Pr(Queen) = (number of cards in each suit)/(total number of cards) = 13/52 = 0.25 = 25%

Sample Space

The set of all possible outcomes of an experiment is called the sample space. The set of all possible outcomes of an experiment are sometimes referred to as the sample space outcomes. This Excel-generated diagram illustrates the sample space of the possible outcomes of the genders of two successive children from a single set of parents:

The preceding diagram is called a Tree Diagram. If the first trial has n₁ possible outcomes and each of those outcomes has the same n₂ possible outcomes, then final total number of possible outcomes for the 2nd trial = n₁ * n₂. In this case n₁ = n₂ = 2. There are 4 possible outcomes in the sample space after the 2^nd trial.

The number of possible outcomes after the kth trial equals n₁ * n₂ * n₃ * … n_k.

Another example would be a man with 2 jackets and 4 shirts. This man has 8 possible shirt-jacket combinations he can choose from.

Event

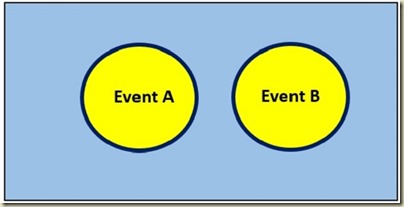
An event is the combination of one or more outcomes that have a single defining characteristic. An event is the set of one or more sample space outcomes that have a defining characteristic. An event derived from the preceding diagram would be the event of at least one of the two children being a girl. This event would be described by the following sample set:

Event A = At least one child is a girl = {BG, GB, GG}

Pr(Event A) = Pr(at least one child is a girl) = Pr(BG) + Pr(GB) + Pr(GG) = 0.25 + 0.25+ 0.25 = 0.75

Another example of an event is the drawing of a red queen from a deck of playing cards. This event is defined the by following set of possible outcomes:

Event A = Red Queen = {Queen of Hearts, Queen of Diamonds}

P(Queen of Hearts) = 1/52 = 0.0192 = 1.92%

P(Queen of Hearts) = P(Queens of Diamonds) = 0.0192

Event A = Drawing a Red Queen = Drawing a Queen of Hearts or Queen of Diamonds

Probability of Event A = Sum of probabilities of outcomes that are described by the event

P(A) = P(Queen of Hearts) + P(Queen of Diamonds)

P(A) = 0.0192 + 0.0192 = 0.0385 = 3.85%

When calculating the probability of a specific event, it is important to determine whether the event is defining by only one single, possible outcomes or if the event is defined by more than two or more unique outcomes of a single trial or experiment.

The probability of Event A is denoted as P(A).

The term event is often used interchangeably with the term outcome, which is used to describe one unique possible outcome of an experiment. Although this is not often done, it is a good idea to specify whether the term event is being used to describe a single, unique outcome or is being used to describe a combination of single, unique outcomes. Note that the formula define the probability of an event use the term E_i to denote outcome i as follows:

Complimentary Event

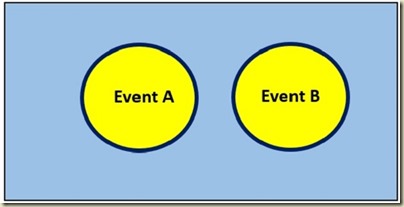
The complimentary event of Event A is the event of an experiment not producing any of the outcomes which define Event A. This is the event of Event A not occurring. The complementary event of event A is denoted as Event . The complimentary event of Event A contains every possible outcome that is not part of the set of outcomes that are associated with Event A. This Excel-generated Venn Diagram illustrates an event and its complementary event:

Event A = Drawing a Red Queen

P(A) = 0.0385

Compliment of Event A = = Not drawing a Red Queen

Sometimes the Compliment of Event A is denoted as A' for ease of presentation because many word processing programs, such as MS Word, do not make it simple to create an overline, i.e., a line over a character.

P(A') = 1 – P(A) = 1 – 0.0385 = 0.9615 = 96.15%

There is a 96.15-percent chance of the compliment of event A not occurring, i.e., that a single card randomly selected from a 52-card deck is not a red queen. Correspondingly, there is a 3.85% chance of event A occurring, i.e., that a single card randomly selected from a 52-card deck is a red queen.

Independent Events

Events are independent of each other is the occurrence of one of the events does not affect the probability of the any of the other events occurring during any successive trials. Events described by the drawing of specific cards from a deck are independent if the drawn card is replaced back into the deck immediately after each draw. If the drawn card is not replaced back into the deck, the events are not independent because of the reduced set of possible outcomes after each draw. Successive flips of a fair coin are independent events.

Short-Term Relative Frequency

The short-term relative frequency = (number of actual occurrences of event)/(actual number of trials)

If 10 flips of a fair coin have produced 2 heads, the short-term relative frequency of heads is 2/10 = .2 = 20%.

Long-Term Relative Frequency

P(E), the calculated expected probability that event E will occur, should always be considered to be a long-term relative frequency. The short-term relative frequency will approach the long-term relative frequency as the number of trials increase. Random variance can cause the short-term frequency to differ significantly from the long-term relative frequency (P(E) – the expected probability).

Mutually Exclusive Events

Events are mutually exclusive of each other if the occurrence of one event precludes the occurrence of any of the other events during a single trial. Events are mutually exclusive if the sample space outcomes that define each event do not contain any of the same individual outcomes that can occur in a single trial. In other words each of the possible outcomes of a single trial is included in the sample set of only one of the events. The event of drawing a red card is mutually exclusive of the event of drawing a black card.

This Excel-generated Venn Diagram illustrates two mutually exclusive events:

This Excel-generated Venn Diagram illustrates two non-mutually exclusive events:

Independence of Events Does Not Mean Mutual Exclusivity of Events, and Vice Versa

Events can be independent and not mutually exclusive. If event A is defined a drawing a Red Queen and Event B is defined as drawing any red card, these event are independent of each other if the drawn card is replaced back in the deck before the next draw. Randomly drawing a Red Queen on the first draw would not change the probability of randomly drawing a red card on the next draw if the first drawn card is replaced back into the deck before the second draw. These events are not mutually exclusive because the events of drawing a red card contains the same set of outcomes that can occur if a Red Queen is drawn.

The events of drawing a red card and drawing a black card are mutually exclusive because none of the outcomes in the sample space of the event of drawing a red card are the same as any of the outcomes in the sample space of the event of drawing a black card. If the first drawn card is not replaced, then the events are not independent of each. The removal of a single red or black card from a deck changes the probability of drawing either a black card or red card on successive draws.

Sampling With Replacement Ensures That Successive Trials Are Independent

When the sample taken is immediately placed randomly back into the population, the population remains unchanged. The probability of any specific outcome remains unchanged in successive trials when the population is returned to its original state as a result of sampling with replacement. The binomial distribution is often used to calculate the probability of a positive binary event occurring when samples are replaced. An example is as follows:

Given a regular deck of 52 playing cards, calculate the probability that 7 out of 10 cards randomly sampled will be red if each sample is immediately replaced before the next one is taken. This probability is calculated using the following Excel formula:

Pr(X ≤ k) = BINOM.DIST(k, n, p, TRUE)

X = the actual number of times a positive binary occurrence (a red card) occurs during the sampling

k = the specified number of positive occurrences (red cards) = 7

n = the sample size = the total number of trials (cards sampled) = 10

p = probability of a positive occurrence = 0.50 = 50% chance of a red card in a regular deck

TRUE indicates the cumulative distribution function, i.e., UP TO 7 red cards in the sample

Pr(X ≤ 7) = BINOM.DIST(7,10,0.50,TRUE) = 0.945313 = 94.53 percent chance of up to 7 red cards in 10 sample drawn from a regular deck if sample are replaced.

Sampling Without Replacement Ensures That Successive Trials Are Not Independent

When the samples replaced back into the population, the population changes after every sample. The current state of the population is dependent on the outcomes of all of the previous samples. Sampling without replacement ensures that successive trials are not independent of each other. The hypergeometric distribution is often used to calculate the probability of a positive binary event occurring when samples are not replaced. An example is as follows:

Given a regular deck of 52 playing cards, calculate the probability that 7 out of 10 cards randomly sampled will be red if samples are not replaced. The probability is calculated using the following Excel formula:

Pr(X ≤ k) = HYPGEOM.DIST(k, n, K, N, TRUE)

X = the actual number of times a positive binary occurrence (a red card) occurs during the sampling

k = the specified number of positive occurrences (red cards) = 7

n = the sample size = the total number of trials (cards sampled) = 10

K = the number of positive occurrences in the population at the start of sampling = 26

N = the population size at the start of the sampling = 52

TRUE indicates the cumulative distribution function, i.e., UP TO 7 red cards in the sample

Pr(X ≤ 7) = HYPGEOM.DIST(7,10,26,52,TRUE) = 0.9624324 = 96.24 percent chance of up to 7 red cards in 10 sample drawn from a regular deck if samples are not replaced.

The Union of Two Events = A OR B = A U B

The union of two events A and B is the probability either A or B will occur. The union or addition of two events is denoted as follows:

Addition of N Mutually Exclusive Events

The addition of mutually exclusive events is calculated by the following formula:

The following Excel-generated Venn Diagram illustrates the addition of two mutually exclusive events.

The Intersection of Two Events = A AND B = A ∩ B

The intersection of two events A and B is the probability of both A and B occurring. The intersection or multiplication of two events is denoted as follows:

P(A₁ ∩ A₂) equals the probability of an object belonging to sets A₁ and A₂.

The following Excel-generated Venn Diagram illustrates the intersection of two events.

Addition of 2 Non-Mutually Exclusive Events

The addition of non-mutually exclusive events is calculated by the following formula:

A₁ ∩ A₂ = A₁ AND A₂ = Intersection between A₁ and A₂ as shown in the following Venn Diagram

The following Excel-generated Venn Diagram illustrates the addition of two non-mutually exclusive events.

For example, in a company of 10,000 employees, it is known that 2,000 employees have at least one green car, 3,000 employees have at least one blue car, and 500 employee have both a green car and a blue car. Calculate the probability of a randomly selected employee owning a green car or a blue car.

Pr(Own a green car) = Pr(Green) = 2,000/10,000 = 0.2

Pr(Own a blue car) = Pr(Blue) = 3,000/10,000) = 0.3

Pr(Own a blue car and own a green car) = Pr(Green ∩ Blue) = 500/10,000 = 0.05

Pr(Green Or Blue) = Pr(Green) + Pr(Blue) – Pr(Green AND Blue)

Pr(Green U Blue) = Pr(Green) + Pr(Blue) – Pr(Green ∩ Blue) = 0.2 + 0.3 – 0.05 = 0.45 = 45%

There is a 45-percent probability that a randomly selected employee owns a green or blue car.

The Intersection of Two Non-Events = A' ∩ B' = (Not A) AND (Not B)

A' ∩ B' = P [ (A' ∩ B' )' ] = 1 – P(A U B)

Conditional Probability

If the occurrence of one event depends upon the occurrence of another event, a conditional probability is created. If the occurrence of event A depends on the occurrence of event B, the conditional probability of event A is denoted as P(A|B), which is stated as the probability of A given B. The formula for P(A|B) is as follows:

For example, 30 people out of a group of 100 exercise regularly. 10 of these exercisers wear Nike shoes. Calculate of a person wearing Nike shoes given that the person exercises regularly.

Event A = A person wears Nikes

Event B = A person exercises regularly

Pr(A) = Pr( Person in the group of 100 wears Nikes) = Not given

P(B) = Pr( Person in the group of 100 exercises regularly) = 0.30

P(A ∩ B) = Pr( Person in the group of 100 wears Nikes AND exercise regularly) = 0.10

P(A|B) = Pr(A ∩ B) / Pr(B) = (0.10) / (0.30) = 1/3 = 0.33 = 33%

33-percent of those in the group of 100 who exercise regularly wear Nikes.

The Multiplication of N Independent Events

Events are either independent or not independent of each other. Events are independent if the occurrence of any event does not affect the probability of the any other events occurring.

Events A and B are independent if the following are true:

P(A|B) = P(A)

or equivalently

P(B|A) = P(B)

The following is the formula for the intersection (AND) of multiple independent events. Note that the probability of the intersection of multiple independent event equals the product of the individual probabilities of each of the events.

For example, what is the probability of a single roll of two dice producing “snake eyes?” The outcome of “snake eyes” occurs when both of the dice are showing a single dot after the roll.

The outcome of separate rolls of dice are independent form each other. The probability of a single dice rolling a 1 is 1/6 = 0.1667 = 16.67%

Event A₁ = Dice 1 rolling a 1

Event A₂ = Dice 2 rolling a 1

Pr(A₁) = Pr(A₂) = 0.1667

Pr(Dice 1 rolling a 1 AND Dice 2 rolling a 1) = Pr(A₁ AND A₂) = Pr(A₁ ∩ A₂) = Pr(A₁) Pr(A₂)

Pr(A₁ ∩ A₂) = Pr(A₁) Pr(A₂) = (0.1667)(0.1667) = 0.0278 = 2.78%

There is a 2.78-percent chance that a single roll of 2 dice will produce “snake eyes.”

The Multiplication of Non-Independent Events

The probability of the intersection of two non-independent events requires the knowledge of the conditional probability of one of the events as follows:

For example,

P(A|B) = Pr(A ∩ B) / Pr(B) = (0.10) / (0.30) = 1/3 = 0.33 = 33%

33-percent of those in the group of 100 wear Nike shoes given they exercise regularly. 30-percent of that group of 100 exercise regularly. What percentage of that group wear Nikes and exercise regularly?

Event A = A person wears Nikes

Event B = A person exercises regularly

Pr(A|B) = Pr( A person wears Nikes given that the person exercise regularly) = 33% = 0.33

Pr(B) = Pr( A person exercises regularly) = 30% = 0.3

Pr(A ∩ B) = Pr(B) * Pr(A|B) = (0.3)*(0.33) = 0.1 = 10%

10-percent of the group of 100 wear Nikes and exercise regularly.

Note that a comparison between the conditional probability calculated previously, Pr(A|B) = 33%, the probability of intersection calculated here, Pr(A ∩ B) = 10%, make a strong implication that Nike is a preferred brand by those who exercise. The larger that group is and the more representative that group is of the general population, the more validity that implication has.

Law of Total Probability

Assume the Events A₁, A₂, .., A_n are mutually exclusive events whose intersection is sample space S. This means that sample space S is entirely composed of these mutually exclusive (non-overlapping) events and nothing else. E represents any of these events. The Law of Total Probability states that the probability of any of these events (Events A₁, A₂, .., A_n) occurring is the following:

P(E) = P(A₁)P(E|A₁) + P(A₂)P(E|A₂) + P(A₃)P(E|A₃) + … + P(A_n)P(E|A_n)

For example, a factory has 4 machines that produce similar items.

The event of any of these machines producing a defect is denoted as Event D.

Machine A₁ produces 40% of all items of which 5% are typically defective.

Machine A₂ produces 30% of all items of which 6% are typically defective.

Machine A₃ produces 20% of all items of which 7% are typically defective.

Machine A₄ produces 10% of all items of which 8% are typically defective.

From this we can state the following:

Probability that an item was made by machine A₁ = 40% so P(A₁) = 0.4

Probability that an item was made by machine A₂ = 30% so P(A₂) = 0.3

Probability that an item was made by machine A₃ = 20% so P(A₃) = 0.2

Probability that an item was made by machine A₄ = 10% so P(A₄) = 0.1

We can also state the following:

Probability that a defect occurred given that the item came from Machine A₁ = P(D|A₁) = 0.05

Probability that a defect occurred given that the item came from Machine A₂ = P(D|A₂) = 0.06

Probability that a defect occurred given that the item came from Machine A₃ = P(D|A₃) = 0.07

Probability that a defect occurred given that the item came from Machine A₁ = P(D|A₄) = 0.08

P(D), the probability that a defect will occur on any of the machines is calculated by the Law of Total Probability as follows:

P(E) = P(A₁)P(E|A₁) + P(A₂)P(E|A₂) + P(A₃)P(E|A₃) + … + P(A_n)P(E|A_n)

P(D) = P(A₁)P(D|A₁) + P(A₂)P(D|A₂) + P(A₃)P(D|A₃) + P(A₄)P(E|A_n)

P(D) = (0.4)(0.05) + (0.3)(0.06) + (0.2)(0.07) + (0.1)(0.8) = 0.06

There is a 6 percent chance that an item produced by any of the 4 machines will be defective.

Bayes’ Theorem

Closely related to the Law of Total Probability is Bayes’ Theorem. Bayes’ Theorem, named after English mathematician Thomas Bayes (1702 – 1761), is sometimes called the theorem on the probability of causes because it calculates the probability of each of the possible causes of an event given that the event occurred.

Assume the Events A₁, A₂, .., A_n are mutually exclusive events whose intersection is sample space S. This means that sample space S is entirely composed of these mutually exclusive (non-overlapping) events and nothing else. E represents any of these events. Bayes’ Theorem calculates P(A_k|E), the probability of a specific event (Ak) occurring given that one of the events did occur, as follows:

P(A_k|E) = P(A_k) * P(E|A_k) / P(E)

Using data from the previous example, calculating the probability that a defect came from a specific machine given that a defect did occur is done as follows:

P(A_k|E) = P(A_k) * P(E|A_k) / P(E)

P(A_k|D) = P(A_k) * P(D|A_k) / P(D)

Recall the following from the previous example:

P(D) = Probability of a defect occurring = 0.06