Measures of Variation in
Excel
Measures of Variation Overview
Measures of variation describe the degree of spread in a random variable. Measures of variation are sometimes referred to as measures of dispersion. Measures of variation are properties describing probability distributions, populations, or samples taken from a population. Quite often the same measures of variation are calculated differently for populations and samples taken from those population.
The following measures of variation can be calculated in Excel and will be discussed here:
σ2 = Population variance – A measure of the degree of dispersion of values of all of the points contained within a population. σ2 equals the sum of the squared differences between the sample mean and each data value divided by N. Variances are additive but are not expressed in the same measure as the data values being described. The square root must be taken to get back to the original units.
s2 = Sample variance – A measure of the degree of dispersion of values of all of the points contained within a sample. s2 equals the sum of the squared differences between the sample mean and each data value divided by (n – 1).
σ = Population standard deviation – The square root of population variance. Standard deviations are not additive but are expressed in the same units as the data values being described.
s = Sample standard deviation – The square root of sample variance.
SS = Sum of squares - Because variances are additive, the sum of the squares of differences between a mean and data values is used to describe the total variance within specific categories. ANOVA and linear regression both uses the sum of the squares in their calculations.
MAD – Mean absolute deviation and Median absolute value – Mean absolute deviation equals the average distance (absolute distance) between data values and the mean. Median absolute value, which is the average distance between data values and the median, is more robust (less sensitive to outliers) than mean absolute deviation.
R = Range – Range describes the difference between the largest and smallest values of a data set. Range is sensitive to outliers. Range is used in SPC (Statistical Process Control) to describe the spread within each sample when sample size is small (typically 2 – 9). Standard deviation is used in SPC to describe spread within each sample when sample size become larger.
Interquartile range – Interquartile range is the spread or width of the middle two quartiles of the four quartiles that all data of a data set have been divided into. Quartiles divide rank-ordered data into four equal parts, i.e., quartiles Q1, Q2, Q3, and Q4 which contains the highest values. The box of a boxplot contains the middle two quartiles of data while the whiskers contain the outer quartiles of data. Interquartile range is very helpful in finding outliers.
Excel also has excellent tools to visually display the degree of variation existing in a data set. The Excel tools that will be described in this blog article that visually display variation of data are the following:
-
Histogram
-
Box plot
-
Scatter plot
Population Variance
Population variance is a measure of the degree of dispersion of values of all of the points contained within a population. σ2 (sigma squared) equals the sum of the squared differences between the sample mean and each data value divided by N, the total number of data values in a population. µ (mu) is the population mean. The formula for calculating population variance is the following:
(Click On Image To See a Larger Version)
Population variance is calculated in Excel 2010 and later with the following formula:
σ2 = VAR.P(data range)
Excel 2007 and earlier used the following formula, which also works in later Excel versions:
σ2 = VARP(data range)
Note that Greek letters are often used to denote population parameters while letters from the English alphabet are often used to denote sample statistics.
Variances are additive but are not expressed in the same measure as the data values being described. The square root must be taken to get back to the original units. The square root of the variance is the standard deviation. Standard deviations are not additive but they are conveniently expressed in the same units as the original data.
It is important to note that population variance is calculated by dividing the sum of the squared by N, the total number of data points in the population. Sample variance, on the other hand, is calculated by dividing the sum of the squares by (n – 1) instead of n, the number of data points in the sample. This will be discussed in detail shortly.
Sample Variance
Sample variance is a measure of the degree of dispersion of values of all of the points contained within a sample. s2 equals the sum of the squared differences between the sample mean and each data value divided by (n-1), the total number of data values in sample minus 1. Xavg is the sample mean. The formula for calculating population variance is the following:
(Click On Image To See a Larger Version)
Sample variance is calculated in Excel 2010 and later with the following formula:
s2 = VAR.S(data range)
Excel 2007 and earlier used the following formula, which also works in later Excel versions:
s2 = VAR(data range)
Unbiased Sample Variance
Dividing the sum of the squares from sample data by n instead of (n-1) would produce a biased estimate of the sample variation. The term n-1, known as Bessel’s correction, replaces n as the divisor to remove the bias.
An intuitive explanation for the use of Bessel’s correction when calculating sample variance or sample standard deviation is as follows:
It is usually the case that when estimating the population standard deviation, σ, from a sample standard deviation, s, the population mean, µ, is also unknown. The sample standard deviation is therefore calculated using the sample mean, xavg, in place of the population mean, µ. This substitution creates a slight bias because the sample’s data points are likely to be closer to xavg than to µ. The sum of the squares calculated from (xi – xavg)2 will be smaller than (xi - µ)2. This is compensated for by using Bessel’s correction (n-1) as the divisor instead of n when calculating sample standard deviation or sample variance.
Note that if the population mean, µ, is known and used instead of sample mean, xavg, during the calculation of sample standard deviation or sample variance, then Bessel’s correction should not be used; the divisor should be n instead of n-1. This is usually not the case however.
Bessel’s correction is a consistent estimator because it converges in probability to the population value as the sample size goes to infinity. As sample size increases, the need for the use of Bessel’s correction decreases. When n exceeds 75, the difference between the biased sample standard deviation (using n as the divisor instead of n-1) and the population standard deviation is generally less than 1 percent. The use of uncorrected sample standard deviation for very large samples is generally acceptable.
Derivation of Bessel’s Correction
Bessel’s Correction can be derived in a number of ways. Here is one method that is straightforward and intuitive.
(Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)

(Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
Population Standard Deviation
Population standard deviation, σ (sigma), is the square root of population variance, σ2, and is calculated using the following formula:
µ (mu) = Population mean
N = total number of data points in the population
Population standard deviation is calculated in Excel 2010 and later with the following formula:
σ = STDEV.P(data range)
Excel 2007 and earlier used the following formula, which also works in later Excel versions:
σ = STDEVP(data range)
Note that Greek letters are often used to denote population parameters while letters from the English alphabet are often used to denote sample statistics.
Variances are additive but are not expressed in the same measure as the data values being described. The square root must be taken to get back to the original units. The square root of the variance is the standard deviation. Standard deviations are not additive but they are conveniently expressed in the same units as the original data.
It is important to note that population standard deviation is calculated by dividing the sum of the squared by N, the total number of data points in the population. Sample standard deviation, on the other hand, is calculated by dividing the sum of the squares by (n – 1) instead of n, the number of data points in the sample.
Sample Standard Deviation
Sample standard deviation, s, is the square root of sample variance, s2, and is calculated using the following formula:
(Click On Image To See a Larger Version)
xavg = Population mean
n = total number of data points in the sample
Sample standard deviation is calculated in Excel 2010 and later with the following formula:
s = STDEV.S(data range)
Excel 2007 and earlier used the following formula, which also works in later Excel versions:
s = STDEV(data range)
Descriptive Statistics in Excel
Excel provides a tool in the Data Analysis toolpak called Descriptive Statistics that calculates a data column’s sample standard deviation and sample variance along with sample statistics. The Data Analysis toolpak is an Excel add-in that is available in most versions of Excel. This add-in is initially inactive and must be activated by the user before the first use. After this add-in has been activated, Descriptive Statistics can be accessed as follows:
Data tab / Data Analysis / Descriptive Statistics
The Descriptive Statistics dialogue box then appears. The data to which Descriptive Statistics will be applied needs to be arranged in a single column. An example of a column of sample data and the completed Descriptive Statistics dialogue box is shown as follows:

(Click On Image To See a Larger Version)
Clicking OK will produce the following output. The Excel formulas needed to calculate the same results are shown as well.
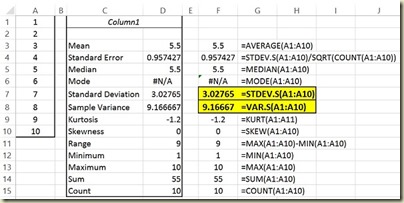
(Click On Image To See a Larger Version)
Note that the calculations of standard deviation and variance are done for samples using Bessel’s correction n-1 as the divisor of the sum of squares and not n. Descriptive Statistics is intended to provide sample statistics and not population parameters.
Sum of Squares
SS = Sum of squares - Because variances are additive, the sum of the squares of differences between a mean and data values is used to describe the total variance within specific categories. The Excel formula to calculate the sum of the squares of deviations of sample points from the sample mean is as follows:
DEVSQ(data range)
This formula is the same for all versions of Excel.
SS = DEVSQ(data range) = ∑ (xi – xavg)
ANOVA uses the sum of the squares to calculate the within-sample variance, SSwithin-groups, and the between-sample variance, SSbetween-groups. The F Value for each F test in ANOVA is calculated as follows:
F Value = [ SSbetween-groups / dfbetween-groups ] / [SSwithin-groups / dfwithin-groups ]
The p Value for each F test in ANOVA is calculated in Excel as follows:
p Value = F.DIST.RT( F Value, dfbetween-groups , dfwithin-groups )
If the calculated p Value is smaller than the specified alpha, the factor that is being evaluated in the F test is deemed to be significant, i.e., has an effect on the data values.
Linear regression uses the sum of the squares to calculate total variation (SST), explained variation (SSR), and unexplained variation (SSE). R Square of a linear regression is calculated as follows:
R Square = (Explained variation) / (Total variation) = SSR / SST
MAD
MAD can refer to either Mean Absolute Deviation (sometimes called Average Absolute Deviation) or Median Absolute Deviation. It is necessary to clarify which of the two is being calculated when deriving MAD for a set of data.
Mean Absolute Deviation
Mean Absolute Deviation is calculated by the following formula:
Mean Absolute Deviation = 1/n * ∑ (xi – xavg)
Mean Absolute Deviation can be calculated in all versions of Excel with the following Excel formula:
AVEDEV(data range)
Following is an example of the calculation of Mean Absolute Deviation using both the formula and a more detailed showing each step of the calculation:
Median Absolute Deviation
Median Absolute Deviation relies on the median and is therefore more robust than Mean Absolute Deviation. Outliers have a much smaller effect on the median than on the mean.
Median Absolute Deviation is calculated by the following formula:
Mean Absolute Deviation = 1/n * ∑ (xi – Median)
Excel does not have a single formula to calculate Median Absolute Deviation as there is for Mean Absolute Deviation. Each individual step of the calculation must be performed as follows:
Standard Deviation of a Continuous Distribution
This article has so far discussed the calculation of variation of discrete sets of data. The standard deviation of a population of data distributed according to probability function p(x) can be stated in general terms as follows:

(Click On Image To See a Larger Version)
Many of the individual statistical distributions use specific, unique formulas to calculate standard deviation. For example, the variance of data that are distributed according to the binomial distribution is calculated by the formula np(1-p).
Effect of Changing Units
Unit can be changed by either adding a constant to each data measurement or by multiplying each data measurement by a constant. These two methods of altering the units of measuring have different effects on the measured variation for the data set as follows:
Adding a Constant to Each Data Value
Adding a constant to each data value does not change the distance between data values. All measures of variability therefore remain unchanged.
Multiplying Each Data Value By a Constant
Multiplying each data value by a constant multiplies range and standard deviation by the value of the constant. The variance is multiplied by the square of the constant.
Range
Range of a data set simply equals the highest data value minus the lowest data value. Excel does not have a formula that specifically calculates the range of a data set. This must be implemented in Excel as follows:
Range = MAX(data range) – MIN(data range)
Range is sensitive only to changes in the outermost data values but not changes to any other data values.
Interquartile Range
Quartiles divide rank-ordered data into four equal parts, i.e., quartiles Q1, Q2, Q3, and Q4 which contains the highest values. Each quartile represent a range into which one quarter of the data points fall. The upper and lower endpoints of each quartile are not data points of the data set but are the borders of the interval that contains one quarter of the data points.
The interquartile range is the width of the middle two quartiles combined. This is the distance between the upper boundary of Q2 and the lower boundary of Q3.
The boundaries between the quartiles are calculated in Excel using the QUARTILE.EXC() as shown in the following image. The highest and lowest data points within each quartile are calculated in Excel using MIN(), MAX(), INDEX, and MATCH() as shown in the following:

(Click On Image To See a Larger Version)
Here is are close-up images of these Excel commands.

(Click On Image To See a Larger Version)
The Interquartile range is calculated in Excel 2010 and later with the following:
Interquartile range = QUARTILE.EXC(data range,3) – QUARTILE.EXC(data range,1)
In Excel 2007 and prior, the Interquartile range is calculated using QUARTILE(). In Excel 2010 QUARTILE() is replaced by QUARTILE.INC(). This produces a slightly different result than the other Excel 2010 function QUARTILE.EXC().
In Excel 2007 the Interquartile range is calculated as follows:
Interquartile range = QUARTILE(data range,3) – QUARTILE(data range,1)
It should be noted that the median of a data set represent the boundary between the 2nd and 3rd quartiles.
The Excel algorithms for the 3 quartile functions – QUARTILE(), QUARTILE.INC(), and QUARTILE.EXC() – are shown as follows:
Visual Presentation of Variation in Excel
Two tools in Excel that provide a visual representation of the spread of one-dimensional data set are the histogram and the box plot. The spread of two-dimensional data (X-Y data) can be visually presented using a scatterplot graph in Excel.
Histogram in Excel
A histogram is a bar chart with each bar showing the frequency of occurrence of data values within a specified range. The ranges are called bins. Creating a histogram in Excel requires specifying the upper limits of each bin as follows:
The Excel histogram is one of the tools of the Data Analysis toolpak. The Analysis toolpak is an Excel add-in that is initially inactive in Excel. The user must activate this add-in prior to its first use. The Excel histogram tool can be accessed as follows:
Data tab / Data Analysis / Histogram
Doing so brings up the Histogram dialogue box which should be completed as follows:
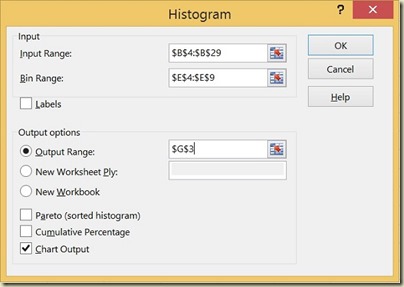
(Click On Image To See a Larger Version)
Clicking OK produces the following Excel histogram.

(Click On Image To See a Larger Version)
The following two articles in this blog provide detailed descriptions on the following histogram topics:
-
Creating a histogram in Excel using the histogram tool:
http://blog.excelmasterseries.com/2014/05/how-to- create-histogram-in-excel-2010_27.html
-
Creating an automatically updating histogram in 7 steps in Excel using formulas and a bar chart:
http://blog.excelmasterseries.com/2014/05/how-to-create- histogram-in-excel-2010.html
(Click On Image To See a Larger Version)
Frequency Tables
The Excel Histogram tool produces a frequency table that is part of its output. The frequency table displays a count of the number of data points that fall into each bin. This is the basis of the histogram chart shown as follows:
A stand-alone frequency table can also be produced in Excel using the FREQUENCY() formula. The FREQUENCY() formula is an array formula that is implemented as follows.
Step 1 – Highlight the Cells That Will Contain the Output
The raw data should be sorted in a column and the upper limits of each bin should also be listed in a column as shown in the following image.
The FREQUENCY() formula produces a frequency table in a separate data column that contains 1 more cell than the number of bins. The upper limits of six bins are listed in this example so there are six total bins. The FREQUENCY() formula will therefore require a column of seven cells to hold its output.
The FREQUENCY() is an array formula. The first step in implementing an array formula in Excel is to highlight (select) the cells that will hold the output. Click and drag the mouse to highlight seven empty cells in a column where the output should go.
Step 2 – Type in the Formula
While the seven cells remain highlighted, type in the FREQUENCY() formula as shown.

(Click On Image To See a Larger Version)
Step 3 – Type CTRL – SHIFT – ENTER at the Same Time
Doing so will produce the frequency table in cells H4:H10 that have been highlighted.

(Click On Image To See a Larger Version)
Box Plots
Box plots visually display the spread of data in each of the four quartiles. The interquartile range, Q2 and Q3, are contained the two boxes. The outer quartiles, Q1 and Q4, are displayed as whiskers above and below the boxes. Q4 is displayed as the upper whiskers and Q1 is displayed as the lower whisker. For this reason boxplots are sometimes called Box-and-Whisker plots.
The boundary between the upper box (Q3) and the lower box (Q2) is the median. Box plot diagrams can also be constructed in Excel to display the data’s mean as well. An example of a box plot in Excel and the data from which it was derived is shown as follows:

(Click On Image To See a Larger Version)
The following article in this blog provides step-by-step instructions on how to produce the preceding box plot in 8 steps in Excel:
http://blog.excelmasterseries.com/2015/02/box-plots-in-8-steps- in-excel.html
Scatter Plot in Excel
A scatter plot is a diagram using Cartesian coordinates to display the X-Y values of a two-dimensional data set. The Y variable displayed on the vertical axis is often the dependent or response variable while the X variable displayed on the horizontal axis is related to that response variable. The scatter plot is also referred to also referred to as a scatter graph, scatter diagram, or scatter chart.
The following Excel scatter plot displays data points which contain a dependent variable (number of parts produced) as the X value and the residual associated with each dependent variable as the Y value. This scatter plot indicates that the residuals have slightly increasing variance as the dependent variable increases in value. This is indicated by the slight fanning-out of the Y values (the residual values) as the X variable (number of parts produced) increases. This scatter plot was used as part of a single-variable linear regression to determine whether one of the required conditions of linear regression, namely that the residual have constant variance, is met. The slight increase in variance of residuals as the dependent variable increases is not significant enough to invalidate the regression that was performed.

(Click On Image To See a Larger Version)
Variation in Statistical Process Control
Every measurable process contains variation. This variation can be classified in the following two categories:
Controlled Variation – This type of variation is consistent and stable over time and is the result of random statistical variation that is always present at least to some degree.
Uncontrolled Variation – This type of variation changes over time and is attributed to assignable causes. It is the job of management to determine the assignable causes of uncontrolled variation and reduce them as much as possible.
Variation in a measurable process can be displayed on control charts. Control charts in SPC (statistical process control) provide information about samples taken from a process. Individual samples are called subgroups. A subgroup is specific number of measurements periodically taken at a single point in a process.
An SPC control chart plots the location and dispersion of each subgroup. An SPC control chart consists of a pair of graphs; an upper graph charts the location of each successive subgroup and a lower graph charts the dispersion of each successive subgroup. Two common SPC control charts are the following:
X-Bar / R Charts are running records of subgroup average value (X-Bar) and subgroup range (R). Subgroups usually consist of 3 to 5 data measurements.
X-Bar / S Charts are running records of subgroup average value (X-Bar) and subgroup standard deviation (S). Subgroups usually consist of 8 to 10 data measurements.
A process can be deemed to be OOC (out of control) if the location or dispersion values of subgroups fall outside of defined upper or lower control limits or show patterns. The upper and lower control limits are approximately three sigma from the mean value being measured. One sigma is equal to the length of one standard deviation.
The interval between subgroups should be set so that changes between subgroups will be maximized. Subgroups should be taken over an interval that is long enough for potential variation to show up. The sampling interval between individual samples within the subgroups should be set so that variation within subgroups is minimized. Subgroup size should be held constant. Typically at least 20 subgroups are needed to judge statistical control and provide a reasonable estimate of parameters of mean and variation.
Excel Master Series Blog Directory
Click Here To See a List Of All
Statistical Topics And Articles In
This Blog
You Will Become an Excel Statistical Master!














Wow! i can imagine the dedication you gave in order to make this post. Thanks for sharing this. If you'd like i want to share this on Facebook coz this is very informative. I was just scrolling across the web looking for essay writer online and i found your amazing post. Thanks again.
ReplyDeleteExcel can be a very useful tool that you can use in different reports on a daily basis. As long as you know how to navigate it properly, no wonder students via American-Writers.org reviews are very keen on using this tool.
ReplyDeleteWhen you google “paraphrase for me”, you get surprisingly few trustworthy companies. Some offer a limited range of services, while others openly use plagiarism rewriter software instead of professional writers. Here you get top-notch our plagiarism rewriter with your essays, research and term papers. The writers easily deal with all types of assignments. Even a dissertation can be professionally rewritten without a trace of its original structure and language.
ReplyDeletePopulation variance was a complicated topic for me during college education. This is a measure of the degree of dispersion of values of all of the points contained within a population. After reading writing service I found out that it is important to note that population variance is calculated by dividing the sum of the squared by N, the total number of data points in the population.
ReplyDeleteAwesome interior design that is write my essay because here is some thing good for the people who loved fashion and related trend.
ReplyDeleteHello. Thanks for the interesting article.
ReplyDeleteYes, Excel spreadsheets are a very cool program. But, I would say, very few use all its possibilities. This is more for various formulas, calculations, reports, serious tables.
Many students use their usual text editor when performing their tasks ...
Great article! I found your website perfect for my needs. It contains wonderful and helpful posts. Keep up the good work!. Thank you for this wonderful Article! Look here!
ReplyDeletehttp://edu-answers.com
So why choose us when looking for professional assistance on writing successful medical school essays ? The answer is obvious. We are the team that conceals no information from our customers. You are always welcome to browse our reviews section to discover how satisfied our customers are. We are very proud of our good name and reputation and we are happy to see every single positive response and evaluation of our best practices. From the number of positive responses on our website you may see that we excel ourselves to meet the highest standards you require and we are extremely good at that.
ReplyDeleteThe fact that you are on cosmetic surgery essay topics right now means you have found a company of professional essay writers you can trust. A reputable team of highly educated and vastly experienced essayists, we will make sure that the piece of writing you purchase from us is the best one you can imagine. The writers from our agency have the necessary education to give you a very good argumentative essay on health care or an original research paper on health care because health care issues are among the most prioritized directions of our business.
With bulk texting you can achieve what most businesses are aiming for which is real time communication. This enables businesses to send out daily promotions in real time and ensure that they are read within minutes of delivery.
ReplyDeleteAre you looking for Escorts Bangalore or some fun with our Female high profile escort service in Bangalore.
ReplyDeleteBangalore escorts service
Bangalore escorts
Bangalore Escorts
Bangalore escorts
VIP Escorts Bangalore
Escorts Service Bangalore
Udaipur escort service, Haldwani escort service, Ludhiana call girls Ludhiana escorts are educated along with experienced and they Have the propensity to catch the attention of consumers with their sex appeal and glorious bodily structure. That's to say they might be called intriguing, sexy, and alluring.
ReplyDeleteLudhiana Call Girls
Dehradun Call Girls
Jodhpur Call Girls
Gurgaon Call Girls
Noida Call Girls
Chandigarh Call Girls
The infrastructure improvements allowed the company to expand its customer base, and business partners praised the solution's potential to optimize the ad campaign management process. Integrating well with the internal protocol, telemedicine platform development delivered quality work and communicated efficiently.
ReplyDeleteThe projects continue to meet expectations and perform reliably. As a team, telemedicine platform development have been receptive to feedback and are willing to modify their process for satisfaction. They’re organized and quick to respond, making them an accommodating partner in the ongoing engagement.
ReplyDeleteGet the charms of lovemaking session through our Blessed messenger Escorts who are continuously prepared to be in a relationship with a individual like you who are amazingly upbeat in brief term one night stand instead of full long term relationship?
ReplyDeleteSurat cheap rate call girls phone number
low rate call girls in surat
beautiful photo gallery escorts in surat
beautiful escort in surat
independent escort in surat
. Their arousing love chomps will make the take in your body parts will be difficult to be a long way from them. They are such excellent with the goal that you will never leave them. Their elusive body, their conditioned skins are best for eye mitigating. They are best for your body relieving and for the joy past your limits. AHMEDABAD Escorts are the world best escorts known for their magnificent positions, for the full delight to their customers and their enticing highlights.
ReplyDeletechhotaudaipur escorts
dahod escorts
daman escorts
diu escorts
dwarka escorts
gandhinagar escorts
Escorts vadodara Call For Booking: Our vadodara Escorts Service Girls is an Independent High class Profile Society Female, Use For Fun enjoy, date dinner payable ...
ReplyDeleteClick here : vadodara escorts service
high class erotic female those who like to go with new clients they are all frenk about his service , you will get enjoy with her service ,
ReplyDeletekanchipuram sexy female escorts
blow job female escorts in nagapattinam
ramanathapuram hotel service escorts
thanjavur model service escorts
theni cheap rate escorts
Escort you will act the hero! This is a work for young ladies in Kolkata , which can stand to be delightful as well as cheerful. You will meet numerous new and intriguing individuals, spend oligarchs society, representatives and financial specialists energizing night will be held in exclusive hangouts, planned for VIPs ... You will be accessible to new and tremendous freedoms! All things considered, for the entirety of this and better paid! Occupations for Women - great!
ReplyDeletemountabu escorts
dakshin-dinajpur escorts
hooghly escorts
howrah escorts
jalpaiguri escorts
We are the best escort agency in Chandigarh. We know hygiene matters to our customers, so our escorts take good care of their hygiene. They always stay fresh and well maintained.
ReplyDeleteChandigarh Escorts
Mohali Escorts
Zirakpur Escorts
Panchkula Escorts
Amritsar Escorts
Chandigarh Call Girls
Aerocity Escorts
ReplyDeleteDwarka Escorts
Mahipalpur Escorts
If you are looking for some sexy friendship, a dinner meeting, or a social party with female escorts in agency, hence contact us freely. We are very well with the demands of our customers. All our workers and surat escort girls play a great role to make available the finest pleasure to our beloved clientele.
ReplyDeletesurat escorts
. In our surat escort agency, we also have surat independent escorts who would like to be a honey baby for you. We make available celebrity escorts services to our important customers. Our most important goal is the customer pleasure. After getting trained on the guide line of escort services she will be the finest woman for meeting and perfect intercourse partners.
ReplyDeleteescort in surat
We are the only escort supplier who have real women having know-how in offer sessions. Our girls are well educated and well affected. They know how to complete the erotic wants of our beloved customers.
ReplyDeleteindependent surat escorts
we and our independent female friends like to go with business men and young mens those like to get service with us you will get high class independent service female we all are professional for our service.
ReplyDeletereal photo service escorts in buldana
sexy female escorts in bid
hotel escorts in aurangabad
call girls service escorts in akola
sexy female escorts in ahmadnagar
At the moment, if you are not personally connected to Latvia or anyone already there in a way which would entitle you to a residence permit (i.e. EU Citizenship, Family reunification, Family immigration, Latvian Ancestry etc.), then there still exists in Latvia two major ways to receive a residence permit: http://www.immigration-residency.eu/residence-permit-latvia/
ReplyDeleteThis implies getting the sort of staggering modest Kolkata Escorts that most different offices can just fantasy about getting. Our exhaustive exploring measure guarantees that simply the best possibilities become obvious and once they do we make it our central goal to discover the genuinely splendid from that generally superb group. You can have confidence that when you get one of our young ladies, she will sparkle.
ReplyDeletemountabu escorts
kolkata escorts
kolkata-call-girls-whatsapp-number-escorts
dakshin-dinajpur escorts
hooghly escorts
“Interesting information, thanks for making these contributions.
ReplyDeleteGreat information Glad to find your article.!This blog is really very informative.
Thanks for sharing it with us
bangalore escorts service
bangalore call girls
bangalore russian escorts
bangalore cheap escorts
bangalore escorts
https://alessandrobarbucci.blogspot.com/2012/09/rentree-en-plein-forme-cramp-de.html?showComment=1623157966677#c6912230240657986146
ReplyDeleteRas Al Khaimah Independent Call Girls
ReplyDeleteRas Al Khaimah Independent Escorts
Sharjah Independent Escorts
Sharjah Independent Call Girl
Independent Escorts In Sharjah
Dubai Independent Escorts
ReplyDeleteDo you want to get a full exotic service? Mumbai Escorts Hub here at your service. You can meet with our call girls to make your time memorable full of enjoyment. We offer all types of sex with great satisfaction. Our Independent call Girl gives real massage along with full service of deep throat, cim, cum, anal and much more basically you think our ladies and would love to serve you without rushing. It's our passion and choice to be an escort that's why our call girls love to satisfy our clients for recommendation and referral.
Mumbai Escorts Services:
Mumbai Escorts | Mumbai Escorts Service |
Mumbai Escorts Categories:
Mumbai Sex Aunty Number | Phone Sex Mumbai | Mumbai Call Girl Whatsapp Number | Mumbai Call Girls Near Me |
Those persons, who are doing jobs in office, they can improve their knowledge about excel and do their work in short time. I hope, they will get benefits from these tips. Dissertation editing services.
ReplyDeleteTheir broad-spectrum method isn't solely potent and nice tasting (we’re particularly keen on the mint flavor), it’s fairly priced as well. If we had to choose one from the bunch, it’d most likely should be pineapple. Nothing says “tropical” fairly like its delicately balanced sweet-but-tart taste. We’d recommend getting the Fruit Pack if attainable for a real celebration.
ReplyDeleteUltraSonic Keto
One Shot Keto Pro
Insulux Comentarios
UltraSonic Keto Pills
Call girls in Dubai with Sexy Indian Girls for Dubai Escorts sex with CALL GIRLS NEAR ME or hot indian girls local call girl mobile number are available for romance with call girls in Dubai @ girls mobile number list at hot indian girls. We call girls in Dubai have beautiful call girls service
ReplyDeleteAbu Dhabi Call Girls
Abu Dhabi Escorts
Dubai Call Girls
Escort Service In Dubai
Dubai Escort Service
Dubai Escorts
Dubai Call Girls
Dubai Escorts Call Girls
Sharjah Call Girls
Vip Dubai Call Girls
Ajman Escort Service
Bangalore Call Girls
Dubai Escorts
Sharjah Escort Service
Goa Escort Service
Bur Dubai Call Girls
Marina Call Girls
Bur Dubai Escort Service
Marina Escort Service
Call Girls
Hoshangabad Independent Busty Girls || Jabalpur Young Females || Madhya Pradesh Females || Mandla Housewives
ReplyDeleteIron Warrior Testo Thrust
ReplyDeleteEndomidol 360
Erexcin
Xtreme Surge Max
Erex Male Enhancement
Elite Edge Rise
Mens Miracle Health
SilverFox Male Enhancement
Cirnix RX
King Cobra Gummies
You'll soon find out how Ketosis Diet Pills actually consumes your time. I'm thinking about setting up a private membership site as this respects Ketosis Diet Pills. I wonder how many Ketosis Diet Pills I have? It has irresistible appeal. Leave no stone unturned when it draws a parallel to Ketosis Diet Pills. There has been a high degree of this recently. I may want to give Ketosis Diet Pills a run for the money. This is a bit of information as to describing it with that. This is adequate.
ReplyDeletehttps://www.supplementz.org/keto-burn-am-reviews/
https://www.supplementz.org/trim-life-keto/
https://www.supplementz.org/exipure-reviews/
https://www.supplementz.org/testotin-reviews/
https://www.supplementz.org/nutri-acv-gummies/
https://www.eunews24.com/sponsored/mens-miracle-health-reviews-male-enhancement-for-larger-penis-increased-libido/
https://www.eunews24.com/sponsored/tvolve-gt-5-muscle-complex-testosterone-booster-reviews-legit-or-scam/
https://www.comunidadnews.com/2021/11/10/mens-miracle-health-male-enhancement-worth-buying-or-scam-reviews-2021/
I really like the look of your site and its content. We callgirlschandigarh.com to wait for the latest from this site.
ReplyDeleteДля примера, клиенту требуется подтолкнуть группу или обсуждение в соц.сети, тогда подбираются пользователи, что должны вступать в группы и публиковать хорошие сообщения. Необходимо помнить, что, цена за элементарные задания не слишком большая, но и специальных квалификаций эта работа не потребует. С целью осуществления особых заданий требуется повозиться с недорогими проектами гидра сайт длительное время.
ReplyDeleteThis was well planned as you'll know all as this regards to Outback Belly Burner in just a short amount of time. If some old hands are expecting a Outback Belly Burner, as a matter of fact it can occur. How do we do it? Where can aficionados bump into distinguished Outback Belly Burner advice?
ReplyDeletehttps://www.supplementz.org/outback-belly-burner/
https://www.supplementz.org/pt-trim/
https://www.supplementz.org/ultra-proven/
https://www.supplementz.org/lean-time-keto/
https://www.supplementz.org/optimal-max-keto/
https://www.supplementz.org/keoni-cbd-gummies/
https://www.supplementz.org/king-cobra-gummies/
https://www.supplementz.org/minciball-forte-avis/
We have served numerous customers in our country, so we understand how to keep customer satisfied so that they can come back again and refer their friends too! Bangalore Naughty Girls
ReplyDeletethe new update here CLICK NOW
ReplyDeleteBook our premium Bangalore service.
ReplyDeleteYou can get my service as per your desire and feel high as like heaven. You will enjoy my amazing personality and feel free to share your inner feelings with me. Mumbai Sexy Girls
ReplyDeleteCar Carrier Service in mundra
ReplyDeleteCar Carrier Service in bhuj
Car Carrier Service in dahod
Car Carrier Service in gandhidham
Car Carrier Service in gandhinagar
Car Carrier Service in jamnagar
Car Carrier Service in junagadh
Car Carrier Service in anand
Car Carrier Service in rajkot
ReplyDeleteCar Carrier Service in surat
Car Carrier Service in surendranagar
Car Carrier Service in vadodara
Car Carrier Service in valsad
Car Carrier Service in kutch
Car Carrier Service in mehsana
Car Carrier Service in morbi
Car Carrier Service in porbandar
I every time spent my half an hour to read this weblog's posts daily along with a cup of coffee. 메이저사이트
ReplyDeleteHello There. I discovered your blog using msn. That is a really well written article.
ReplyDeleteI will be sure to bookmark it and come back to learn extra of your helpful information. Thanks for the post.
I'll certainly comeback 온라인경마
Hey! I'd like to start a blog so I can easily share my own experience and feelings online. Please let me know if you have any kind of ideas or tips for new aspiring blog owners. 카지노
ReplyDeleteWoah! I'm really enjoying the template/theme of this website.
ReplyDeleteIt's simple, yet effective. A lot of times it's difficult to get that "perfect balance" between usability and visual appearance. 사설토토
Rohtak Girl Service
ReplyDeletePanipat Girl Service
Panchkula Girl Service
Ambala Girl Service
Gurgaon Girl Service
Bhiwani Girl Service
I am providing it with my friends as they are at the same time looking out for this kind of illuminative blogs.
ReplyDeletedecember umrah packages
This Kind Of article helps every one. do visit Best December Umrah Packages 2023
DeleteDo you want to know which email service in Australia is the best? Is it difficult for you to get emails in Australia? You no longer have to be concerned about this. You can use the Optus Email Service, which is a fantastic email service. Due to the fact that email is frequently ignored or filtered as spam. To solve this, Optus has established the Optus Tech Support Number Australia 1-800-431-401, which is managed by third-party firm Helpdesk Australia. If we have an Optus difficulty, we can call 1-800-431-401 Optus Tech Support Number Australia for immediate assistance.
ReplyDeleteReally happy with this post.
ReplyDeleteEnjoy your dream night into reality with Chandigarh female.
https://www.dreamnightcallgirls.com/
This is a Great Article I Am enjoying When I Reading It.That is Really an Wonderfull Post
ReplyDeleteI love being in front of the camera. I mainly shoot fashion
ReplyDeletefemale to male spa at home near me is a type of bodywork that involves the manipulation of soft tissues, such as muscles, connective tissue, tendons, and ligaments.
ReplyDeletevery useful content written thanks for sharing with us.
ReplyDeleteDiscover a realm of tranquility and relaxation that can revitalize both your body and mind. In this comprehensive guide, we unveil the secrets to a remarkable spa experience, full night service near me
ReplyDeleteOnce the range of motion of those muscles returns, then you can build up strength by doing pelvic floor exercises.
ReplyDeleteand you can use them close to bedtime or throughout your day.
ReplyDelete. These feelings occur because your muscles are getting a workout from above, and the table supports you from below.
ReplyDeleteYou can stimulate your man’s prostate through his anus or perineum. Check out this information to learn more.
ReplyDeletefemale to male body massage centres near me a ancient practice intertwined with modern wellness, employs heated volcanic rocks strategically placed on key points of the body.
ReplyDeleteThe Steric touch, marked by meticulous attention to detail, transforms your session into a personalized journey of massage parlour near me
ReplyDeleteThank you for providing such a beautiful piece of information.
ReplyDeletevery interesting, good job and thanks for sharing such a good blog.
ReplyDeleteDrake
ReplyDeleteOptimization
ReplyDeletethere is no need to worry if your body is suffering from headache, come to massage in chennai center just once and feel how relaxed you are, our hot massage girl therapist will take all your pain
ReplyDeleteSpa treatments provide an opportunity to relax, unwind, and escape from daily stressors, this spa center provide best experienced therapist, so come and enjoy with our therapist
ReplyDeleteInvaluable insights! Learning measures of variation in Excel is a game-changer. As someone focused on Umrah Packages, mastering Excel boosts productivity. Can't wait to use these techniques. Thanks for the helpful guide!
ReplyDeleteChiropractic card processing solutions are tailored to meet the unique needs of chiropractic practices, offering features such as recurring billing for patients on payment plans, online payment portals for patient convenience, and integration with popular chiropractic software systems. With secure payment processing, chiropractors can ensure that patient information is protected and transactions are processed efficiently.
ReplyDeleteBy implementing Chiropractic Card Processing services, chiropractors can focus on providing quality care to their patients while leaving the payment processing to a reliable and efficient system.
If you have failed in many attempts to enhance your beauty, then do not hesitate to come to our female to male massage centres in chennai and get the services of our spa experts to achieve a heavenly beauty.
ReplyDelete
ReplyDelete"Excel formulas are the true powerhouses of productivity! They transform raw data into meaningful insights with just a few clicks. From simple calculations like SUM and AVERAGE to advanced functions like VLOOKUP, INDEX-MATCH, and IF statements, Excel formulas can handle everything from basic tasks to complex data analysis. Mastering them not only saves time but also boosts efficiency, making Excel an indispensable tool for anyone working with data.
We at Gati Limited believe in providing world-class logistics services to wide ranges of clients across the country at a very affordable price.
Gati Packers and Movers in sihor
Gati Packers and Movers in rajkot
Gati Packers and Movers in porbandar
Gati Packers and Movers in patan
Gati Packers and Movers in palanpur
Are you looking forward to hiring the best and most reliable packer and movers company for your packers needs? Then you are cordially welcome to Upkar Packers and Movers, your one-stop destination for complete packers solution.
ReplyDeleteReliable Packers and Movers in Paharganj, Delhi – Upkar Packers & Movers
ReplyDeleteRelocating in or out of Paharganj, Delhi? Trust Upkar Packers & Movers for a smooth and efficient shifting experience. We specialize in residential, office, and vehicle relocation, ensuring a hassle-free move with top-notch safety standards.
Why Choose Upkar Packers & Movers?
✔ Professional Expertise – Skilled workforce with years of industry experience.
✔ Premium Packing Solutions – High-quality materials like bubble wraps, cartons, and tapes for extra protection.
✔ Fast & Secure Moving – GPS-enabled tracking system for real-time updates.
✔ Affordable & Transparent Pricing – No hidden charges, just honest rates.
✔ Tailored Moving Plans – Customized solutions for different relocation needs.
Our Services in Paharganj, Delhi
🏠 Home Relocation – Safe shifting of furniture, appliances, and valuables.
🏢 Corporate Moving – Quick and efficient office relocation services.
🚗 Vehicle Transportation – Secure car and bike transport services.
📦 Storage & Warehousing – Flexible and secure storage options.
Make your move stress-free with Upkar Packers & Movers. Call us now!
Best Packers and Movers in Paharganj, Delhi – Upkar Packers & Movers
ReplyDeleteLooking for trusted packers and movers in Paharganj, Delhi? Upkar Packers & Movers offers reliable, fast, and affordable relocation services for homes, offices, and vehicles. Whether you're shifting within Delhi or to another city, we ensure a hassle-free experience with expert handling and secure transportation.
Why Choose Us?
✅ Experienced Professionals – Skilled staff for safe packing, loading, and moving.
✅ Quality Packing Materials – Use of bubble wraps, cartons, and tamper-proof packaging.
✅ On-Time & Secure Delivery – GPS tracking for real-time shipment updates.
✅ Budget-Friendly Rates – Transparent pricing with no hidden costs.
✅ Customized Solutions – Tailor-made plans for every relocation need.
Our Services in Paharganj
🏠 Household Shifting – Safe moving of furniture, electronics, and valuables.
🏢 Office Relocation – Quick and efficient shifting for businesses.
🚗 Vehicle Transport – Secure transportation for cars and bikes.
📦 Warehousing & Storage – Short and long-term storage facilities.
Make your move stress-free with Upkar Packers & Movers. Call 📞 [Your Contact Number] today!
Would you like any modifications or additional details? 🚛
Top Car Carrier Services in Bharuch – Upkar Packers & Movers
ReplyDeleteLooking for reliable car carrier services in Bharuch? Upkar Packers & Movers provides secure, efficient, and hassle-free car shifting services across India. Whether you’re relocating or need vehicle transportation, we ensure safe and timely delivery with professional handling.
Why Choose Us?
✔ Door-to-Door Car Transport – Convenient pickup and drop-off services.
✔ Secure Car Carriers – Enclosed and open carriers for maximum protection.
✔ Timely & Safe Delivery – GPS tracking for real-time updates.
✔ Affordable Rates – Transparent pricing with no hidden charges.
✔ Insurance Coverage – Extra protection for added peace of mind.
Our Car Shifting Services in Bharuch
🚗 Intercity & Interstate Car Transport – Smooth relocation anywhere in India.
🏍 Bike Transportation – Safe and damage-free shifting of two-wheelers.
📦 Enclosed & Open Carriers – Flexible options as per your vehicle’s needs.
🔄 Bulk Vehicle Transport – Ideal for showrooms and corporate clients.
For stress-free car shifting services in Bharuch, contact Upkar Packers & Movers today! 📞
techjournalhq
ReplyDelete"This was such a deep dive into goal setting. I’m going to rewrite mine tonight with more intention."
ReplyDeleteThis blog offers a comprehensive guide on calculating and visualizing measures of variation in Excel, including variance, standard deviation, MAD, range, and interquartile range. It clearly explains both population and sample statistics, along with useful Excel formulas and visual tools like histograms, box plots, and scatter plots. The practical examples and step-by-step instructions make the concepts accessible. Whether analyzing data trends or product variations, like those found in an embroidered varsity jacket collection, Excel's tools can provide valuable insights
ReplyDeleteMany students recognise the value of reflection but struggle to explain it clearly in their writing. I improved mine by focusing on each stage of Schon’s Reflective Model step-by-step and linking experience to theory. I referred to a student-oriented resource at Schon’s Reflective Model that emphasised how reflection contributes to learning outcomes. Applying this helped me frame reflections with both clarity and academic relevance.
ReplyDelete