The t Test in Excel
Can Determine What Your
Best Sales Days Are
It's always great to know what day of the week you can expect to get peak sales. The t test in Excel can provide that information for you. It's quite a simple test to run, as you will see. This blog article will walk you step-by-step through a t Test in Excel. The t Test compares two groups of samples and determines whether the mean of one sample is different than the other. Most types of t Tests require that each sample group have the same number of samples and also have the same variance. This Excel t Test has neither of those requirements.
Here is the scenario we are going to test: Suppose that you have been monitoring your daily sales for about a year. Your two best sales during the week are normally Monday and Wednesday. You would like to know which of those two days really does produce the best sales. You've tracked Monday sales for the last 40 weeks and Wednesday sales for the last 42 weeks. Mean sales for Wednesday is a bit higher than mean sales for Monday, but you would like to know with 95% certainty whether the difference in means is not just by chance and that Wednesday really is a better day for selling.
You can run your data through an Excel t Test and know within a minute whether Wednesday really is the best sales day. Excel has several built-in t Tests. The specific Excel t Test we will use is called the "t Test: Two Sample Assuming Unequal Variances." This t Test allows for two samples that have unequal sizes and variances. The only requirement is that both samples are Normally distributed. This will be discussed shortly. In Excel 2003, this test can be accessed through this menu path: Tools / Data Analysis / t Test: Two Sample Assuming Unequal Variances. Before we perform this t Test, we need to have a discussion of what the t Test is.
t Test - General Description
This test will tell you whether the difference between the before and after numbers is genuine or whether this difference could merely have been the result of chance. Overall a t-test compares two means and determines within a specified degree of certainty whether the two means really are different, or whether the difference might have occurred by chance.t Test for Two Samples Having
Unequal Sizes and Variances
The t Test that can be applied to two samples with unequal sizes and unequal variances determines whether the means of both samples are the same. In other words, this test evaluates within a specified degree of certainty whether the measured difference between the meaqns is real or could have occurred merely by chance.Before we start discussing this specific test in detail, The t-test needs to be generally explained. The basic question to be answered is:
The t test is a statistics test generally used to test whether means of populations are different. In the t test, a t value is calculated based upon the difference in the means and variances of the two populations. The greater the t value, the more certain it is that the means are different.
The t value can be generally described as follows:
t value = (Difference between the group means) / (Variability of the groups)
There are many variations of the t test. Each has its own specific formula for calculating a t value for the sampled data sets. All of the t value formulas can be described by the above formula.
The Higher the t Value - The More Likely the Groups Are Different
The higher the t value is, the more likely it is that the two means are different. If the two groups being compared have a high degree of variance (t value has a high denominator), it is much harder to tell them apart. On the other hand, if the two groups being compared have a low degree of variance (the t value has a low denominator), it is much easier to tell the two groups apart.The Lower the Combined Variance, the Higher the t Value
The illustrations below should clarify how the degree of variance in the two groups determines how easy or difficult it is to state that the means of the two groups are really different. The t test quantifies this relationship and provides a way to determine whether the measured difference between two means can be considered real or not based upon the amount of variance in both groups. Here are illustrations that should clarify this relationship.The t Test for comparing two samples with unequal sizes and variance is a variation of the t Test called Welch's t Test. It is not the classic Student's t Test, which does not allow for samples having unqual variances.
We are going to use this t test to determine within 95% certainty whether the means sales from Wednesdays is different than the mean sales from Monday. We have measured from the last 42 Wednesdays and the last 40 Mondays and we will apply this Excel t test to determine whether the measured difference between the means is real or not.
A Little Bit More About This t Test
The t Test in general is a special case of one-way (sometimes called “single factor”) ANOVA. This paired two-sample student’s t test is applied when there is a natural pairing of samples. It is most often used to determine whether “before” and “after” means of a sample of the same objects have changed during an experiment. One really great thing about this t test is that the paired two-sample t test does not require that the variances of both populations to be the same.Here is the formula to calculate the t value for a two-sample t test of unequal variances if you are testing to determine whether there difference between the two samples:
t value = [ X1 - X2 ] / [ SQRT( (s1^2 / n1) + (s2^2/n2) ) ]
Degree of Freedom = df =
[ [ (s1^2 / n1) + (s2^2 / n2) ]^2 ] / [ ( [ (s1^2 / n1)^2 ] / [n1 -1 ] ) + ( [ (s2^2 / n2)^2 ] / [n2 -1 ] ) ]
X1 and X2 are the sample means. s1 and s2 are the sample standard deviations, and n1 and n2 are sample sizes.
You can see that this follows the general formula for calculating the t value in a t test, which is:
t value = (Difference between the group means) / (Variability of the groups)
The t value is a specific point on the x-axis in the t distribution (student’s t distribution). If this t value falls outside the region of required certainty, it can be stated that the two means are probably different. If this t value falls within the region of required certainty, it cannot be stated that the two means are probably different.
The required region of certainty depends upon the degree of certainty required in the test. If 95% certainty is required, then the required region of certainty consists of 95% of the area under the student’s t distribution. The outer 5% is the region of uncertainty. This is also referred to as α (alpha) or the degree of significance. If the t value is large enough to be located all the way out on the x-axis in the 5% region of uncertainty, it can be stated within 95% certainty that the two means are different.
A t test can be a one-tailed test or a two-tailed test. A one-tailed test determines whether the means are different in one specific direction. For example, a one-tailed test could be used to determine only if the mean of the “after” measurements is greater than the mean of the “before” measurements. A two-tailed test determines whether the two means are merely different.
Two-Tailed t Test Is More Stringent
The two-tailed test is more stringent because the area in the outer tails outside of the region of required degree of certainty is split into two tails. For example, if the required degree of certainty is 95% on a two-tailed test, the calculated t value must be all the way out in the outer 2.5% of either tail for the t test to conclude within 95% certainty that the means are different.
One-Tailed t Test Is Less Stringent
A one-tailed test is less stringent. If the required degree of certainty is 95% on a one-tailed test, the calculated t value only has to be within the outer 5% of whatever tail is being tested to be able to state the two means are probably different.We are testing to determine whether there really is a difference between mean sales on Monday and mean sales on Wednesday.
The data need to be arranged in Excel as follows:
The t Test we are about to use allows for different sample sizes and different variances, but that standard requirement for all t Tests is that both samples being compared are Normally distributed. There are a number of different ways of doing this. For brevity, we are going to do it the simplest possible way. We will make an Excel histogram of each sample's data and simple eyeball the shape of the histogram. If the shape of each histogram resembles the Normal curve, we will go with it.
There are a number of better ways of checking for Normality and here is a link to an article in this blog which describes how to do a simple but more accurate Excel Normality test called the Normal Probability Plot.
The Excel histogram is a simple thing to construct. If you haven't ever done one, here is a link to an article in this blog which shows how to create a histogram in Excel from sample data.
Completed histograms for each of the two samples are as follows:
Both histograms appear to be Normally distributed so we can use t Test to compare the two samples. If either sample is not Normally distributed, the t test cannot be used because the output is likely to be totally incorrect. If either sample is not Normally distributed, we must use a nonparametric test such as the Mann-Whitney U Test to compare the samples.
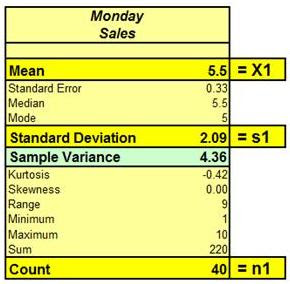
Before we run the t Test, we would like to take a look at a description of of each sample. In Exzcel 2003, this can be quickly done by the following tool: Tools / Data Analysis / Descriptive Statistics. The Descriptive Statistics for each sample are as follows:
Now, access this Excel t Test as follows (this is Excel 2003):
Tools / Data Analysis / t-Test: Two Sample Assuming Unequal Variances
This following dialogue box will appear:
Input the data as followings:
Variable 1 Range: Select everything that is highlighted yellow, including the label “Monday Sales.”
Variable 2 Range: Select everything that is highlighted tan, including the label “Wednesday Sales.”
Hypothesized Mean Difference: 0
Labels: Check the box because you included the labels for Variables 1 and 2.
Alpha: This depends on your desired degree of certainty. 0.05, if you desired 95% certainty. 0.20 if you desire 80% certainty.
Output Range: Select the cell that you want the upper left corner of the output to appear in.
Hit “OK” to run the analysis and the following Excel output appears:
This output can be interpreted as follows:
The t value is -6.088.
α = 0.05 = 1 - Required Degree of Certainty = 1 - 95%
p Value (1-Tailed) = 1.88E-08
p Value (2-Tailed) = 3.77E-08
This t value has a greater absolute value (6.088) than the critical t value for a one-tailed test (1.664). We can therefore state with 95% certainty that there really is a difference between Wednesday sales and Monday sales.
The above conclusion can also be reached because the p Value for the one-tailed test (highlighted in light red on the Excel output) is 1.88E-08. This is much less than alpha (0.05). The p Value being less than alpha is an equivalent result to the t value being greater than the t critical value.
The same result is arrived at for the two-tailed test. The two-tailed test is more stringent because the alpha region of uncertainty (5% of the area under the student’s t distribution curve) is now divided between both outer tails. The t value needs to be larger for the two-tailed test to wind up in the outer 2.5% area of either outer tail.
In this case, the t value was large enough to be positioned in the outer 2.5% of either outer tail. The absolute value of t value (6.088) is much larger than the critical t value for the two-tailed test (1.990). This indicates that it can be stated with 95% certainty that there really is a difference between Wednesday sales and Monday sales in this case as well.The p value calculated for the two-tailed test (3.77E-08) is much smaller than alpha (0.05). This is an equivalent result to the above.
Let’s calculate the t value and p values for the one and two-tailed tests by hand to make sure that Excel has done a correct job. The t value is stated as the t statistic.
Here is the original test data Excel Descriptive Statistics:
Here is the hand calculation of the t value and p values for the one and two-tailed tests for this Two-Sample t Test Assuming Unequal Variance. The hand calculations below of the t Value and p Values agree with the Excel outputs. There are very slight differences due to rounding differences:
t value = [ X1 - X2 ] / [ SQRT( (s1^2 / n1) + (s2^2/n2) ) ]
Degree of Freedom = df =
[ [ (s1^2 / n1) + (s2^2 / n2) ]^2 ] / [ ( [ (s1^2 / n1)^2 ] / [n1 -1 ] ) + ( [ (s2^2 / n2)^2 ] / [n2 -1 ] ) ]
The Degrees of Freedom calucation must be rounded to the nearest whole number, which in this case is 80.
X1 and X2 are the sample means. s1 and s2 are the sample standard deviations, and n1 and n2 are sample sizes.
p Value = TDIST ( T Statistic, df, Number of Tails )
Here are the actual calculations done by hand in Excel:
The Two Sample t Test Assuming Unequal Variances.is a very simple test to run in Excel and can be applied to nearly any aspect of your marketing program to see if one group of samples is different from another group of samples. One note: both sample groups must be continuous and measured using the using the same scale.

Please post any comments you have on this article. Your opinion is highly valued!
Excel Master Series Blog Directory
Statistical Topics and Articles In Each Topic
- Histograms in Excel
- Bar Chart in Excel
- Combinations & Permutations in Excel
- Normal Distribution in Excel
- Overview of the Normal Distribution
- Normal Distribution’s PDF (Probability Density Function) in Excel 2010 and Excel 2013
- Normal Distribution’s CDF (Cumulative Distribution Function) in Excel 2010 and Excel 2013
- Solving Normal Distribution Problems in Excel 2010 and Excel 2013
- Overview of the Standard Normal Distribution in Excel 2010 and Excel 2013
- An Important Difference Between the t and Normal Distribution Graphs
- The Empirical Rule and Chebyshev’s Theorem in Excel – Calculating How Much Data Is a Certain Distance From the Mean
- Demonstrating the Central Limit Theorem In Excel 2010 and Excel 2013 In An Easy-To-Understand Way
- t-Distribution in Excel
- Binomial Distribution in Excel
- z-Tests in Excel
- t-Tests in Excel
- Overview of t-Tests: Hypothesis Tests that Use the t-Distribution
- 1-Sample t-Tests in Excel
- Overview of the 1-Sample t-Test in Excel 2010 and Excel 2013
- Excel Normality Testing For the 1-Sample t-Test in Excel 2010 and Excel 2013
- 1-Sample t-Test – Effect Size in Excel 2010 and Excel 2013
- 1-Sample t-Test Power With G*Power Utility
- Wilcoxon Signed-Rank Test As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
- Sign Test As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
- 2-Independent-Sample Pooled t-Tests in Excel
- Overview of 2-Independent-Sample Pooled t-Test in Excel 2010 and Excel 2013
- Excel Variance Tests: Levene’s, Brown-Forsythe, and F Test For 2-Sample Pooled t-Test in Excel 2010 and Excel 2013
- Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro Wilk Tests For Two-Sample Pooled t-Test
- Two-Independent-Sample Pooled t-Test - All Excel Calculations
- 2-Sample Pooled t-Test – Effect Size in Excel 2010 and Excel 2013
- 2-Sample Pooled t-Test Power With G*Power Utility
- Mann-Whitney U Test in Excel as 2-Sample Pooled t-Test Nonparametric Alternative in Excel 2010 and Excel 2013
- 2-Sample Pooled t-Test = Single-Factor ANOVA With 2 Sample Groups
- 2-Independent-Sample Unpooled t-Tests in Excel
- 2-Independent-Sample Unpooled t-Test in Excel 2010 and Excel 2013
- Variance Tests: Levene’s Test, Brown-Forsythe Test, and F-Test in Excel For 2-Sample Unpooled t-Test
- Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro-Wilk For 2-Sample Unpooled t-Test
- 2-Sample Unpooled t-Test Excel Calculations, Formulas, and Tools
- Effect Size for a 2-Independent-Sample Unpooled t-Test in Excel 2010 and Excel 2013
- Test Power of a 2-Independent Sample Unpooled t-Test With G-Power Utility
- Paired (2-Sample Dependent) t-Tests in Excel
- Paired t-Test in Excel 2010 and Excel 2013
- Excel Normality Testing of Paired t-Test Data
- Paired t-Test Excel Calculations, Formulas, and Tools
- Paired t-Test – Effect Size in Excel 2010, and Excel 2013
- Paired t-Test – Test Power With G-Power Utility
- Wilcoxon Signed-Rank Test As a Paired t-Test Alternative
- Sign Test in Excel As A Paired t-Test Alternative
- Hypothesis Tests of Proportion in Excel
- Hypothesis Tests of Proportion Overview (Hypothesis Testing On Binomial Data)
- 1-Sample Hypothesis Test of Proportion in Excel 2010 and Excel 2013
- 2-Sample Pooled Hypothesis Test of Proportion in Excel 2010 and Excel 2013
- How To Build a Much More Useful Split-Tester in Excel Than Google's Website Optimizer
- Chi-Square Independence Tests in Excel
- Chi-Square Goodness-Of-Fit Tests in Excel
- F Tests in Excel
- Correlation in Excel
- Pearson Correlation in Excel
- Spearman Correlation in Excel
- Confidence Intervals in Excel
- Overview of z-Based Confidence Intervals of a Population Mean in Excel 2010 and Excel 2013
- t-Based Confidence Intervals of a Population Mean in Excel 2010 and Excel 2013
- Minimum Sample Size to Limit the Size of a Confidence interval of a Population Mean
- Confidence Interval of Population Proportion in Excel 2010 and Excel 2013
- Min Sample Size of Confidence Interval of Proportion in Excel 2010 and Excel 2013
- Simple Linear Regression in Excel
- Overview of Simple Linear Regression in Excel 2010 and Excel 2013
- Simple Linear Regression Example in Excel 2010 and Excel 2013
- Residual Evaluation For Simple Regression in Excel 2010 and Excel 2013
- Residual Normality Tests in Excel – Kolmogorov-Smirnov Test, Anderson-Darling Test, and Shapiro-Wilk Test For Simple Linear Regression
- Evaluation of Simple Regression Output For Excel 2010 and Excel 2013
- All Calculations Performed By the Simple Regression Data Analysis Tool in Excel 2010 and Excel 2013
- Prediction Interval of Simple Regression in Excel 2010 and Excel 2013
- Multiple Linear Regression in Excel
- Basics of Multiple Regression in Excel 2010 and Excel 2013
- Multiple Linear Regression Example in Excel 2010 and Excel 2013
- Multiple Linear Regression’s Required Residual Assumptions
- Normality Testing of Residuals in Excel 2010 and Excel 2013
- Evaluating the Excel Output of Multiple Regression
- Estimating the Prediction Interval of Multiple Regression in Excel
- Regression - How To Do Conjoint Analysis Using Dummy Variable Regression in Excel
- Logistic Regression in Excel
- Logistic Regression Overview
- Logistic Regression Performed in Excel 2010 and Excel 2013
- R Square For Logistic Regression Overview
- Excel R Square Tests: Nagelkerke, Cox and Snell, and Log-Linear Ratio in Excel 2010 and Excel 2013
- Likelihood Ratio Is Better Than Wald Statistic To Determine if the Variable Coefficients Are Significant For Excel 2010 and Excel 2013
- Excel Classification Table: Logistic Regression’s Percentage Correct of Predicted Results in Excel 2010 and Excel 2013
- Hosmer-Lemeshow Test in Excel – Logistic Regression Goodness-of-Fit Test in Excel 2010 and Excel 2013
- Single-Factor ANOVA in Excel
- Overview of Single-Factor ANOVA
- Single-Factor ANOVA Example in Excel 2010 and Excel 2013
- Shapiro-Wilk Normality Test in Excel For Each Single-Factor ANOVA Sample Group
- Kruskal-Wallis Test Alternative For Single Factor ANOVA in Excel 2010 and Excel 2013
- Levene’s and Brown-Forsythe Tests in Excel For Single-Factor ANOVA Sample Group Variance Comparison
- Single-Factor ANOVA - All Excel Calculations
- Overview of Post-Hoc Testing For Single-Factor ANOVA
- Tukey-Kramer Post-Hoc Test in Excel For Single-Factor ANOVA
- Games-Howell Post-Hoc Test in Excel For Single-Factor ANOVA
- Overview of Effect Size For Single-Factor ANOVA
- ANOVA Effect Size Calculation Eta Squared (?2) in Excel 2010 and Excel 2013
- ANOVA Effect Size Calculation Psi (?) – RMSSE – in Excel 2010 and Excel 2013
- ANOVA Effect Size Calculation Omega Squared (?2) in Excel 2010 and Excel 2013
- Power of Single-Factor ANOVA Test Using Free Utility G*Power
- Welch’s ANOVA Test in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
- Brown-Forsythe F-Test in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
- Two-Factor ANOVA With Replication in Excel
- Two-Factor ANOVA With Replication in Excel 2010 and Excel 2013
- Variance Tests: Levene’s and Brown-Forsythe For 2-Factor ANOVA in Excel 2010 and Excel 2013
- Shapiro-Wilk Normality Test in Excel For 2-Factor ANOVA With Replication
- 2-Factor ANOVA With Replication Effect Size in Excel 2010 and Excel 2013
- Excel Post Hoc Tukey’s HSD Test For 2-Factor ANOVA With Replication
- 2-Factor ANOVA With Replication – Test Power With G-Power Utility
- Scheirer-Ray-Hare Test Alternative For 2-Factor ANOVA With Replication
- Two-Factor ANOVA Without Replication in Excel
- Creating Interactive Graphs of Statistical Distributions in Excel
- Interactive Statistical Distribution Graph in Excel 2010 and Excel 2013
- Interactive Graph of the Normal Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Chi-Square Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the t-Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Binomial Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Exponential Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Beta Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Gamma Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Poisson Distribution in Excel 2010 and Excel 2013
- Solving Problems With Other Distributions in Excel
- Solving Uniform Distribution Problems in Excel 2010 and Excel 2013
- Solving Multinomial Distribution Problems in Excel 2010 and Excel 2013
- Solving Exponential Distribution Problems in Excel 2010 and Excel 2013
- Solving Beta Distribution Problems in Excel 2010 and Excel 2013
- Solving Gamma Distribution Problems in Excel 2010 and Excel 2013
- Solving Poisson Distribution Problems in Excel 2010 and Excel 2013
- Optimization With Excel Solver
- Maximizing Lead Generation With Excel Solver
- Minimizing Cutting Stock Waste With Excel Solver
- Optimal Investment Selection With Excel Solver
- Minimizing the Total Cost of Shipping From Multiple Points To Multiple Points With Excel Solver
- Knapsack Loading Problem in Excel Solver – Optimizing the Loading of a Limited Compartment
- Optimizing a Bond Portfolio With Excel Solver
- Travelling Salesman Problem in Excel Solver – Finding the Shortest Path To Reach All Customers
- Chi-Square Population Variance Test in Excel
- Analyzing Data With Pivot Tables
- SEO Functions in Excel
- Time Series Analysis in Excel
















Đặt vé máy bay tại Aivivu, tham khảo
ReplyDeletekinh nghiệm mua vé máy bay đi Mỹ giá rẻ
vietnam airlines quốc tế
đặt vé máy bay từ đức về việt nam
lịch bay hà nội moscow
vé máy bay từ anh về việt nam
vé máy bay từ pháp về việt nam giá rẻ
khách sạn cách ly hà nội
ve may bay chuyen gia nuoc ngoai
Writing a dissertation is a serious scientific work that takes time. The terms for the creation of such material start from 6 months. If you want to get a job faster, make a request at https://essaywriter.org/term-paper-for-sale We will evaluate the terms you are interested in and give you an answer before ordering. If our authors cope with the work in the time you need, we will be able to fulfill your request
ReplyDelete