Wednesday, March 24, 2010

Regression - The Two Crucial Steps to Excel Regression That Most People Skip

Regression Analysis

Done in Excel

2 Most Important Steps



Running a Regression in Excel is fairly easy. So is running one incorrectly. There are two crucial steps that should always be performed on the data before any Regression should be run. Fortunately these two steps are very quick and easy to do in Excel. They are:

1) Graph the Data
2) Run Correlation Analysis On All Variables

Here is a video of this article showing how to perform all four steps to Regression in Excel, including the above two crucial steps at the beginning:


Step-By-Step Video Showing How To Do All 4 Steps of Regression in Excel, Including the 2 Crucial Initial Steps That No One Does, But Should

(Is Your Sound Turned On?)




Why You Need To Run The 2 Crucial Steps Before Doing Regression

Here’s why you need to run the two crucial steps prior to regressing any data in Excel:



Crucial Step 1) Graphing the Data

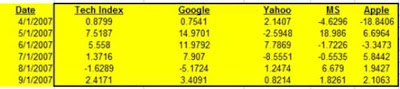
Whether or not you are using Excel to run a Regression, you should always graph the data before doing anything else. Eyeballing the data will allow you to quickly determine whether there is any relationship between the independent (input) variables and the dependent (output) variable. You also want to evaluate whether the graph generally appears to be linear or possibly quadratic. Excel’s Regression Tool works well only for reasonably linear data. Eyeballing the data upfront will tell you very quickly whether Excel’s Linear Regression is the right tool for the job.


Graphing The Data To Check If It Is Linear
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View

The input and output variables will be graphed together. The y-axis of the chart will provide the scale for plotting of those values. The x-axis will provide a measure of whatever continuum was used, e.g. time, to collect the values of all of the variables. Excel’s charting function is the way to go here. The above linked video shows exactly how to chart all the data in Excel.



Crucial Step 2) Running Correlation Analysis on All Variables Simultaneously

There are two good reasons for doing this. First, we want to remove any input variables which are clearly not good predictors of the output variable. Second, we want to make sure that none of the input variables have a high correlation with (are good predictors of) other input variables.

Running Correlation Analysis on the Data To Prevent Collinearity and also To Remove Input Variables That Have Low Correlation With the Output Variable
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View

Correlation of multiple variables is easily done in Excel using the Correlation Data Analysis tool. The linked video shows exactly how to do that.


Remove Input Variables That Have Low Correlation With Output Variable

After you have run Correlation Analysis on the data, you will want to remove any input variables that have a low correlation with the output variable. A Correlation Coefficient of with an absolute value of less than 0.4 (between -0.4 and +0.4) between the output variable and an input variable indicates that the input variable is not a good predictor of the output. That input variable should be removed from the Regression Analysis. The attached video provides an example of this.



Data Columns Before Removing Input Variable With Low Correlation To Output

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


Data Columns After Removing Input Variables With Low Correlation To Output

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View



Remove Inputs Variables Highly Correlated With Other Input Variables

After looking at the Correlation Coefficients between the input and output variables, look at the Correlation Coefficients between the input variables themselves. You do not want to use pairs of input variables that are good predictors of each other in a Regression. This will cause a Regression error known as Collinearity or Multicollinearity. One variable from any pair of highly-correlated input variables should be removed prior to running the Regression Analysis. Variables can be considered highly-Correlated if the absolute value of their Correlation Coefficient is greater the 0.7 (greater than +0.7 or less than -0.7).



Adding New Input Variables To The Regression Analysis

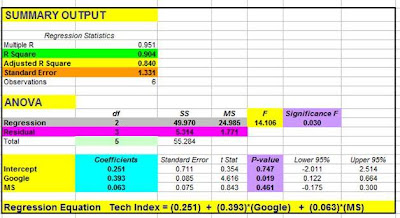
Here are a few hints about adding new input variables to a Regression Analysis. First, build up a Regression by starting with a small number of input variables and add any new ones one at a time. Second, good new input variables noticeably increase Adjusted R Square and also lower Standard Error without significantly changing the existing Regression Coefficients.

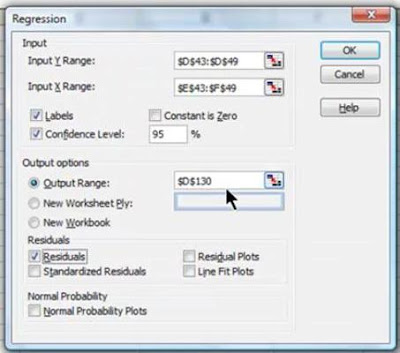
When you are satisfied with the output of the data graph and the Correlation Analysis, go ahead and run the Regression with Excel. An example of how to do this is shown in the above video.


The Excel Regression Dialogue Box
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View




The final step of Excel Regression is Analysis of the Excel output. Here is a link to another video which shows you how to quickly read the most important parts of the Excel Regression output: http://bit.ly/Quickly-Understanding-Excel-Regression-Output



Excel Regression Output With Color Coding Added
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View



Conclusion - Plotting the Data and Running Correlation Can Be BIG Time Savers

Plotting the data and running Correlation Analysis prior to running a Regression can save you lots of time that you might otherwise have to spend making adjustments to your Regression after running it.



regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel



If you have any comments about this article, feel free to post them right here. Your input and opinions are highly valued!



If You Like This, Then Share It...
Dig this Stumble upon regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at
Labels: , , , ,

2 comments:

  1. Bryn_officeteamJune 19, 2010 at 11:37 AM

    Thank you for this great post on regression in Microsoft Excel! Regression is a very popular function in Excel and I am sure many users could benefit from seeing this post!

    Have you joined the community of Excel users over on Facebook?
    I am sure they would love to hear all of your tips and tricks:
    http://www.facebook.com/microsoftexcel

    Cheers,
    Bryn
    MSFT Office Outreach Team

    ReplyDelete
  2. Mark HarmonJune 19, 2010 at 4:51 PM

    Thanks Bryn! I had no idea there was such a group. I'm really looking forward to checking it out.

    ReplyDelete

Subscribe to: Post Comments (Atom)