Thursday, March 18, 2010

Regression - How To Quickly Read the Output of Excel’s Regression

Regression Analysis

Done in Excel

How To Read the Output




There is a lot more to the Excel Regression output than just the regression equation. If you know how to quickly read the output of a Regression done in, you’ll know right away the most important points of a regression: if the overall regression was a good, whether this output could have occurred by chance, whether or not all of the independent input variables were good predictors, and whether residuals show a pattern (which means there’s a problem).



Excel Regression Output With Color-Coding Added

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


This video will illustrate exactly how to quickly and easily understand the output of Regression performed in Excel:


Step-By-Step Video About How To Quickly Read and Understand the Output of Excel Regression

(Is Your Sound Turned On?)


The 4 Most Important Parts of Regression Output
1) Overall Regression Equation’s Accuracy
(R Square and Adjusted R Square)

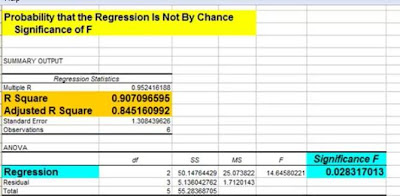
2) Probability That This Output Was Not By Chance
(ANOVA – Significance of F)

3) Individual Regression Coefficient and Y-Intercept Accuracy


4) Visual Analysis of Residuals

Some parts of the Excel Regression output are much more important than others. The goal here is for you to be able to glance at the Excel Regression output and immediately understand it, so we will focus our attention only on the four most important parts of the Excel regression output.

1) Overall Regression’s Accuracy

 
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


R Square– This is the most important number of the output. R Square tells how well the regression line approximates the real data. This number tells you how much of the output variable’s variance is explained by the input variables’ variance. Ideally we would like to see this at least 0.6 (60%) or 0.7 (70%).


Adjusted R Square – This is quoted most often when explaining the accuracy of the regression equation. Adjusted R Square is more conservative the R Square because it is always less than R Square. Another reason that Adjusted R Square is quoted more often is that when new input variables are added to the Regression analysis, Adjusted R Square increases only when the new input variable makes the Regression equation more accurate (improves the Regression equations’s ability to predict the output). R Square always goes up when a new variable is added, whether or not the new input variable improves the Regression equation’s accuracy.



2) Probability That This Output Was Not By Chance

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


Significance of F – This indicates the probability that the Regression output could have been obtained by chance. A small Significance of F confirms the validity of the Regression output. For example, if Significance of F = 0.030, there is only a 3% chance that the Regression output was merely a chance occurrence.


3) Individual Regression Coefficient Accuracy

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View

P-value of each coefficient and the Y-intercept – The P-Values of each of these provide the likelihood that they are real results and did not occur by chance. The lower the P-Value, the higher the likelihood that that coefficient or Y-Intercept is valid. For example, a P-Value of 0.016 for a regression coefficient indicates that there is only a 1.6% chance that the result occurred only as a result of chance.



4) Visual Analysis of Residuals

Charting the Residuals
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


The Residual Chart
regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel
Click On Image To See Enlarged View


The residuals are the difference between the Regression’s predicted value and the actual value of the output variable. You can quickly plot the Residuals on a scatterplot chart. Look for patterns in the scatterplot. The more random (without patterns) and centered around zero the residuals appear to be, the more likely it is that the Regression equation is valid.


There are many other pieces of information in the Excel regression output but the above four items will give a quick read on the validity of your Regression.

regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel



If anyone has any comments or observations related to this article, feel free to submit them because your input and opinions are highly valued.



If You Like This, Then Share It...
Dig this regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel Technorati regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel regression, multiple regression, regression model, regression excel, regression analysis, multiple regression, regression coefficient, statistical analysis in excel

Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at
Labels: , , , , , ,

30 comments:

  1. AnonymousNovember 23, 2010 at 9:46 PM

    Thank you so much for this!!! Very helpful

    Mallory Wood

    ReplyDelete
  2. AnonymousJanuary 13, 2011 at 6:27 PM

    Really nice.

    ReplyDelete
  3. AnonymousApril 17, 2011 at 2:50 PM

    Cheers! [A deadline has been made]

    ReplyDelete
  4. AnonymousApril 28, 2011 at 9:40 PM

    Fantastic post. Am seriously considering buying the entire package.

    regards
    jan/

    ReplyDelete
  5. Vi$hy vi$hJune 29, 2011 at 2:40 AM

    Really good work...helped a lot....
    Thank you ....

    ReplyDelete
  6. AnonymousJuly 9, 2011 at 12:31 AM

    Thank you so much. Very helpful.

    ReplyDelete
  7. AnonymousNovember 17, 2011 at 8:35 PM

    uda man, test saver

    ReplyDelete
  8. AnonymousDecember 15, 2011 at 11:35 AM

    nice and clear! other blogs are so deep into explaining the equations - this is one of the only ones I've seen that actually helps interpret the output in plain language! thanks!

    ReplyDelete
  9. AnonymousJanuary 15, 2012 at 6:15 AM

    very simply and useful.. thanks

    ReplyDelete
  10. AnonymousFebruary 20, 2012 at 3:50 AM

    thank you so much you.... have saved my grade

    ReplyDelete
  11. Mark HarmonFebruary 24, 2012 at 12:43 PM

    Why thanks! Really glad you found it useful. :>D

    ReplyDelete
  12. AnonymousMarch 15, 2012 at 8:35 AM

    Really, really helpful. Thanks!!

    ReplyDelete
  13. AnonymousMarch 19, 2012 at 4:44 AM

    Thanks very much for sharing the knowledge...it was really helpful!

    ReplyDelete
  14. AnonymousMarch 20, 2012 at 6:51 PM

    Working on an assignment for class. This helped more than my notes! Thanks!

    ReplyDelete
  15. AnonymousJuly 2, 2012 at 8:05 AM

    Thanks so much, this was easy to understand. A suggestion though...it would be nice to see this same analysis done with something that isn't highly correlated. The contrast would be helpful in finding simple pitfalls.

    ReplyDelete
  16. AnonymousAugust 1, 2012 at 2:01 PM

    This is great, thank you! I am familiar with diff. analytics terms but not in too much technical terms, so this is very helpful for me!

    ReplyDelete
  17. AnonymousOctober 2, 2012 at 12:28 PM

    Thank you sooo much. im a psych scholar and this helped me finish my thesis in time!
    God bless you!

    ReplyDelete
  18. ShyamOctober 14, 2012 at 7:32 AM

    Thanks a ton buddy...this is really helpful

    ReplyDelete
  19. AnonymousOctober 20, 2012 at 7:17 AM

    This was a great help dear, thanks a lot.

    ReplyDelete
  20. AnonymousJanuary 30, 2013 at 9:29 PM

    Thanks i found it useful. I am obliged.

    ReplyDelete
  21. AnonymousFebruary 16, 2013 at 6:20 AM

    Thank you so much for this information. I've been searching for a while for simple explanations on the regression summary output in Excel and I finally ran across this site. Absolutely a life saver!!

    ReplyDelete
  22. AnonymousMarch 10, 2013 at 5:42 PM

    Fantastic! Very very useful!

    ReplyDelete
    Replies
    1. AnonymousApril 17, 2013 at 5:04 AM

      Does your text cover Excel 2010?

      Delete
  23. AngeloMay 7, 2013 at 10:09 AM

    Awesome dude. Thanks much

    ReplyDelete
  24. AnonymousAugust 1, 2013 at 7:47 AM

    Thank you very much!!! i had trouble understanding what the figures meant and this was very helpful.

    ReplyDelete
  25. HassanOctober 8, 2013 at 1:12 AM

    Thanks a ton !

    ReplyDelete
  26. Tarun BabbaarApril 6, 2014 at 9:15 PM

    To the point and simple...Thanks!

    ReplyDelete
  27. AnonymousMay 21, 2014 at 3:24 PM

    I concur with pretty much everyone who has commented before me...very useful.....thank you

    ReplyDelete
  28. UnknownJune 5, 2014 at 1:52 AM

    is there any one help me to say what is the menaing of p value 0.20

    ReplyDelete
  29. vé máy bay từ canada về việt namAugust 31, 2021 at 7:05 PM

    Đặt vé tại phòng vé Aivivu, tham khảo

    vé máy bay đi Mỹ giá rẻ

    ve may bay tu my ve vietnam

    các chuyến bay từ narita về hà nội

    vé máy bay từ đức về sài gòn

    vé máy bay từ Toronto về việt nam

    vé máy bay từ hàn quốc sang việt nam

    danh sách khách sạn cách ly tại quảng ninh

    vé máy bay chuyên gia nước ngoài sang Việt Nam

    ReplyDelete

Subscribe to: Post Comments (Atom)