Simplifying Excel Ranking
Functions: RANK(),
RANK.AVG(), RANK.EQ(),
PERCENTILE(),
PERCENTILE.INC(),
PERCENTILE.EXC(),
QUARTILE(), QUARTILE.INC
(), QUARTILE.EXC()
Simplifying RANK(), RANK.EQ(), and RANK.AVG()
Ranking functions RANK(), RANK.EQ(), and RANK.AVG() return the rank of a data value within a data set. Prior to Excel 2010 RANK() was the sole ranking function. In Excel 2010 and beyond RANK() will still work but its functionality has been duplicated by a new ranking function RANK.EQ(). In addition, another useful ranking function RANK.AVG() has been added.
The format of each of these functions is as follows:
RANK(value to be ranked, data range, [order])
RANK.EQ(value to be ranked, data range, [order])
RANK.AVG(value to be ranked, data range, [order])
The value to be ranked is a specific number or value is a data set that will be ranked. The data range represents the set of values that will provide the basis for the ranking. The order is an optional value. Setting the order to 0 or leaving it blank will rank data in descending order, i.e., the highest value in the data range will be assigned a rank = 1. Setting the order to 1 will rank data in ascending order, i.e., the lowest value in the data range will be assigned a rank = 1.
The difference between RANK.EQ() and RANK.AVG() is how tied data values within the data set are ranked. RANK.EQ() assigns the lowest rank of the tied values to all of the tied values. RANK.AVG() assigns the average rank of the tied values to all of the tied values.
RANK.AVG() is useful when performing certain nonparametric tests in Excel. Several nonparametric tests require that data be ranked with tied data values being assigned the average rank of the tied values as is done by RANK.AVG(). These nonparametric tests include the Mann-Whitney U Test, the Wilcoxon Signed-Rank Test, and the Friedman Test.
The functionality of the RANK() function is shown as follows. The raw data that is being ranked has already been sorted in order to more easily convey the functionality of the RANK() function.
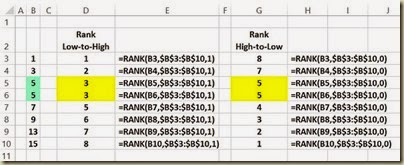
(Click On Image To See a Larger Version)
The functionality of the RANK.EQ() function is shown in the following diagram. RANK.EQ() is equivalent to RANK() and should now be used in its place. Note that tied data values are all assigned the lowest rank of the tied values. The raw data that is being ranked has already been sorted in order to more easily convey the functionality of the RANK.EQ() function.
(Click On Image To See a Larger Version)
The functionality of the RANK.AVG() function is shown in the following diagram. Note that tied data values are all assigned the average rank of the tied values. There is no equivalent to this function in versions of Excel prior to 2010. The raw data that is being ranked has already been sorted in order to more easily convey the functionality of the RANK.AVG() function.
(Click On Image To See a Larger Version)
Simplifying PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC()
Percentile functions PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC() return the value at a given percentile in relation to a given data set. For example, given the data set {1, 3, 5, 13, 15} in cells A2:A6, PERCENTILE(A2:A6,0.3) = 3.4. This means that the value 3.4 occupies the 30th percentile of the given data set.
An example of the use of the percentile functions would be to determine which test scores within a group of test score are at or above the 95th percentile of the group. The percentile functions would return that value that would occupy that 95th percentile of the group.
The percentile functions are typically used to establish a threshold of acceptance or failure.
Prior to Excel 2010 PERCENTILE() was the sole percentile function. In Excel 2010 and beyond PERCENTILE() will still work but its functionality has been duplicated by a new percentile function PERCENTILE.INC(). In addition, another percentile function PERCENTILE.EXC() has been added.
The format of each of these functions is as follows:
PERCENTILE(data range, percentile)
PERCENTILE.INC(data range, percentile)
PERCENTILE.EXC(data range, percentile)
The percentile can be any number between 0 and 1.
The value to be ranked is a specific number or value is a data set that will be ranked. The data range represents the set of values that will provide the basis for the ranking. The order is an optional value. Setting the order to 0 or leaving it blank will rank data in descending order, i.e., the highest value in the data range will be assigned a rank = 1. Setting the order to 1 will rank data in ascending order, i.e., the lowest value in the data range will be assigned a rank = 1.
Both PERCENTILE.EXC() and PERCENTILE.INC() and its equivalent PERCENTILE() first rank the values in the given data set from 1 (assigned to the lowest value in the data set) to n (assigned to the highest value in the data set). The rank K is then calculated. The main difference between is the method of calculating K as shown in the following Excel algorithms for these functions. If K is not an integer value, linear interpolation between the nearest values in the data set to determine the value that would occupy the given percentile.
Another difference between the percentile functions is that PERCENTILE.EXC only works if k is between 1/n and 1-1/n, where n is the number of elements in array. PERCENTILE.INC works for any value of k between 0 and 1.
The Excel algorithm for equivalent functions PERCENTILE() and the equivalent PERCENTILE.INC() is as follows:
(Click On Image To See a Larger Version)
The Excel algorithm for PERCENTILE.EXC() is as follows:
(Click On Image To See a Larger Version)
Simplifying PERCENTRANK(), PERCENTRANK.INC(), and PERCENTRANK.EXC()
PERCENTRANK(), PERCENTRANK.INC(), and PERCENTRANK.EXC() are the inverse functions of PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC().
PERCENTRANK(), PERCENTRANK.INC(), and PERCENTRANK.EXC() return the percentile that a given data value has in relation to set of data values.
PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC() return the data value that would occur at a given percentile in relation to a set of data values.
The following diagram shows the relationship of the PERCENTRANK functions to the PERCENTILE functions. In each of these cases the percentile is the 30th percentile.
(Click On Image To See a Larger Version)
Simplifying QUARTILE(), QUARTILE,INC(), and QUARTILE.EXC()
The quartile functions are special cases of the percentile functions. The equivalent functions are as follows:
QUARTILE(Data range, 0) = PERCENTILE(Data range, 0) = MIN(Data range)
QUARTILE(Data range, 1) = PERCENTILE(Data range, .25)
QUARTILE(Data range, 2) = PERCENTILE(Data range, .5) = MEDIAN(Data range)
QUARTILE(Data range, 3) = PERCENTILE(Data range, .75)
QUARTILE(Data range, 4) = PERCENTILE(Data range, 1) = MAX(Data range)
QUARTILE.INC(Data range, 0) = PERCENTILE.INC(Data range, 0)
QUARTILE.INC(Data range, 1) = PERCENTILE.INC(Data range, .25)
QUARTILE.INC(Data range, 2) = PERCENTILE.INC(Data range, .5)
QUARTILE.INC(Data range, 3) = PERCENTILE.INC(Data range, .75)
QUARTILE.INC(Data range, 4) = PERCENTILE.INC(Data range, 1)
QUARTILE.EXC(Data range, 0) = PERCENTILE.EXC(Data range, 0)
QUARTILE.EXC(Data range, 1) = PERCENTILE.EXC(Data range, .25)
QUARTILE.EXC(Data range, 2) = PERCENTILE.EXC(Data range, .5)
QUARTILE.EXC(Data range, 3) = PERCENTILE.EXC(Data range, .75)
QUARTILE.EXC(Data range, 4) = PERCENTILE.EXC(Data range, 1)
The Excel algorithm for equivalent functions QUARTILE() and the equivalent QUARTILE.INC() is as follows:
(Click On Image To See a Larger Version)
The Excel algorithm for QUARTILE.EXC() is as follows:
(Click On Image To See a Larger Version)
Excel Master Series Blog Directory
Click Here To See a List Of All
Statistical Topics And Articles In
This Blog
You Will Become an Excel Statistical Master!
Not really much of a formula user in excel because I only know the basics. But with these tips on how to simplifying excel ranking functions, it will be more easy for me to generate reports. Glad I came across this view original source.
ReplyDeleteGreat post! I hope it will be useful for me as I don't wan to pay someone to write my research paper. I'd rather research and write by myself.
ReplyDeleteYour substance is out and out splendid from multiple points of view. I think this is connecting with and enlightening material. Much obliged to you such a great amount for thinking about your substance and your perusers. blog comments
ReplyDeleteThis is a brilliant blog! I'm very happy with the comments!.. posizionamento nei motori di ricerca
ReplyDeleteThanks for taking the time to discuss this, I feel strongly about it and love learning more on this topic. If possible, as you gain expertise, would you mind updating your blog with more information? It is extremely helpful for me.
ReplyDeletepikdo
Thank you for sharing information. Wonderful blog & good post.
ReplyDeleteSony WALKMAN App
As a data analyst at Cheap Assignment Writing Services, I am very grateful for making this useful post. Many people struggle about how to find the rank of students in a class, but they didn't get to read like this.
ReplyDeleteThere is no limit for using of mobile phones and the device will be with the people at all the time. So the mobile marketing which targets the audience or users of active internet users and non-active internet users on their mobile phones. data science course syllabus
ReplyDeleteI am really appreciating very much by seeing your interesting posts.
ReplyDeleteHow To Fix AOL Mail Not Working On MacBook Pro
Additionally, shrewd businesspeople may consider opportunities to invest in overseas businesses without actually forming their own companies. In these situations, it still benefits the investor to team up with a knowledgeable adviser in global economics and litigation. International investments create a truly diverse portfolio that offers opportunities for growth that were unthinkable just decades ago. http://www.confiduss.com/en/jurisdictions/mauritius/business/company-formation/
ReplyDeleteAfrican Mango Seed Extract Market is often combined with other ingredients such as green tea and marketed as a fat-burning supplement. Because of the weight-loss properties associated with the seed extract, along with the rising fears about health problems such as obesity, the market for African mango seed extract is expected to be further propelled forward. The industry is also being driven by the rising demand for foods made from natural ingredients.
ReplyDeleteThe total land area of Japan is 377,915 km² (approx. 145,913 mi²). and the total exclusive economic zone (EEZ) is 4,479,388 km² (~1,729,493 mi²). The continental shelf of Japan is approximately 454,976 km² (around 175,666 mi²). Including land mass and EEZ, the total area of Japan is approximately 4,857,303 km² (~1,875,407 mi²). Japan is considered to be a large nation because of its total area. http://www.confiduss.com/en/jurisdictions/japan/geography/
ReplyDelete@Fantasy Power 11 You can play every day online, live carrom board games. if you have a strong knowledge of carrom.
ReplyDeleteCarrom Board Online, top carrom games, play carrom board, carrom board game online, carrom game online at best carrom games app for android phones to earn real money
Cash and the amount to be approved in your bank or Paytm wallet immediately.
Carrom Board Online
ReplyDeleteThere is an inborn curiosity about the Love Marriage Astrology, and Astrology can do it for you. Click here to know "predict my life partner free". You can also book a direct appointment to bail out of all the issues.
You made some good points there. I searched on google about this topic and found that most of the people will believe your blog… If you are planning to travel to kenya with kenya e visa, you should read the guidelines of evisa kenya online.
ReplyDeletegoogle 258
ReplyDeletegoogle 259
google 260
google 261
google 262
Nice Blog! the content you have provided is very informative. Thank you for this blog. Click here to get the solutions for the AOL Mail Not Working Issue.
ReplyDeleteThis is a topic that’s near to my heart… Many thanks! Where are your contact details though? E Visa for India is you can obtain online without the need of visiting the Indian Embassy and Consulate. India business visa cost depends on your country, you can check india visa site online. You can apply for india business visa registration via mobile phone, computer or desk.
ReplyDeleteWonderful blog! you have shared informative blog. It would be very beneficial for everyone. Excel is very important for everyone. Get the solution for Change Verizon Email Password of your account.
ReplyDeleteThe guy that order essay online is free from using such functions
ReplyDeleteThank God my parents didn’t force me to choose statistics as my subject even though they wanted me to but I knew I can never comprehend it. I’m happy with my literature subject where I read, write, and sometimes even get to Buy Assignment uk services when needed. So; I’m living a stress-free life.
ReplyDeleteIf someone works on excel function correctly the task become time efficient, just like any essay help canada .
ReplyDeleteI definitely enjoy every little bit of it. This is a great website and good stock. I want to thank you… South Africa study visa, South Africa is a wonderful country to explore and make a career.
ReplyDeleteI am very thankful for such a wonderful blog. It's very interesting to read and easy to understand. Thanks for sharing. I will visit your blog daily because I know. It may be very beneficial for me. If you want to Fix QuickBooks Online Error Code 101 please contact quickbooks team for instant help.
ReplyDeleteWe are an online academic assistance provider that is focused helping students to score well in their college assignments. We are providing assignment help services on Supply Chain Management assignment to students studying in Australia and other nations.
ReplyDeleteWow.. Very informative article thanks for sharing please keep it up.. Indian tourist evisa in 2022 starts issuing long term visas to those who want to travel in India.
ReplyDeleteThis is promissing and there can be advantage of having a best and nice thing that have been achieved within the time and we can increase the system.
ReplyDeleteVip Girls Service in Delhi
Hii sir, Good info for a new blogger...it's really helpful. e tourist visa India fees UK, You can check tourist visa India fees on our website.
ReplyDeleteHi! Do you know basically something about sic bio?I play live sic bo online on 9winz where I could play this game, the mose colossal for me is speedy withdrawal. Compassionately associate with me in the event that you have any censure.
ReplyDeleteErectile Dysfunction (ED) is considered the most common sexual health problem men report to their doctors. ED is said to affect as many as 30 million men nationwide. Find treatment for ED today when you schedule a free consultation with Prime Men's Medical Center.
ReplyDeleteThe simplifying method where Someone Write My Assignment similar to the above content
ReplyDeleteI'm appreciative for every one of your information, Site is an outstandingly very enlightening substance.
ReplyDeleteHigh Profile Girls in Bangalore
High Profile Girls in Bangalore
High Profile Girls in Bangalore
High Profile Girls in Bangalore
High Profile Girls in Bangalore
We are in charge of some of the most respected Islamic websites in Pakistan and throughout the world. If you want to learn more about Islam & the Quran or any other topic, follow this link to our website. You may also use our app to improve both your life and your IQ.
ReplyDeleteThanks for sharing these shortcuts for excel as a students it is very important to know these kind of tips to save our time because students nowadays are getting a lot of work to do from there school and colleges they have to write assignments and there homework which is very time taking if anyone is looking for assignment and Online Homework Help then they can contact Global Assignment Help USA They offer services at affordable rates to help students achieve A+ grades.
ReplyDeleteAs the largest city in New England, Boston is home to a large and diverse population of people from all walks of life. And with so many different cultures and religions represented, finding a place to pray can sometimes be a challenge. But never fear! We've got you covered with our comprehensive guide to boston prayer times in 2022.
ReplyDeleteThanks a lot for writing this great piece of writing. I needed to find an article on this subject, and you helped me do that.
DeleteUwatchfreemovies
Turkish series
The verse exhorts believers to recognise and take advantage of their blessings from Allah. The PDF version of Surah Rahman also exhorts believers to have patience and have faith in Allah's purposes. The Surah Rahman PDF concludes with the promise that those who remain obedient would receive Allah's greatest mercy and recompense.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteFantastic article. Your works are distinctive, easy to understand, and contain informative and inspiring material. Keep up the fantastic work!
ReplyDeleteThank you very much for your amazing blog.
ReplyDeleteMuslim Names are the name that adheres to the naming standards established by Islam and has a meaning that is suitable for the individual. Discover well-known Islamic names beginning with a variety of alphabets, with options for both boys and girls, so you can choose the perfect moniker for your new little darling. On hamariweb, you'll find a massive collection of modern, trendy, and famous Muslim Names for children. From this extensive list, you can choose the name that is most fitting for your child.
ReplyDeleteFrom timeless classics to modern blockbusters, The Movie Outfits have left an indelible mark on American fashion. Think about Marilyn Monroe's iconic white dress in "The Seven Year Itch" or the sleek black suits of the Men in Black.
ReplyDeletentroducing Leather Blazer Men, the epitome of sophistication and timeless style. In the USA, these iconic garments have become a popular choice for those seeking a refined and polished look.
ReplyDeleteGoogle Australia is like your laid-back Aussie mate who knows all the ins and outs of the land Down Under. It's your go-to for finding the best surfing spots, uncovering hidden gems in the Outback, or even just translating Aussie slang. From kangaroos to Vegemite, Google Australia is here to help you embrace the true Aussie spirit.
ReplyDeleteHire Williams Wall Heater Installation Los Angeles service in California for getting your AC & heater repaired and maintenance. Just check our website and place your order now.
ReplyDeleteWant to buy diazepam kaufen? If yes, then Ams Farm is one of the best online pharmacy store where you can order and purchase online medicine at an affordable price. For getting more information, visit our website now.
ReplyDeleteLook no further than Mens Leather Jacket With Hood These statement pieces offer the perfect combination of edgy and practical. From chilly days to unexpected rain showers, these jackets have got you covered in style. Elevate your outerwear game now!
ReplyDeleteAdd a touch of sophistication to your wardrobe with our Leather Blazer Men, available in the USA. These sleek and stylish blazers are crafted from premium leather, offering a luxurious and refined look. Perfect for both formal and casual occasions, our leather blazers elevate your style game with their timeless appeal.
ReplyDeleteThe Fast And Furious Outfits collection is a must-have for fans of the franchise and fashion enthusiasts alike. With their sleek lines, bold colors, and attention-grabbing details, these outfits bring the excitement of the movies to your wardrobe. Strap in, ignite your style, and prepare for an adrenaline-fueled fashion experience like no other.
ReplyDeleteOh, let me tell you about Eddie Munson Vest! It's a total showstopper. Picture a vibrant explosion of colors and patterns, all skillfully woven together. It's like a wearable work of art that never fails to turn heads and spark conversations. Eddie's got style, that's for sure!
ReplyDeleteExcel ranking functions, RANK(), RANK.AVG(), RANK.EQ(), PERCENTILE(), PERCENTILE.INC(), PERCENTILE.EXC(), QUARTILE(), QUARTILE.INC(), QUARTILE.EXC()
ReplyDeleteExcel is a powerful tool for data analysis and decision-making. However, when it comes to ranking and percentile calculations, things can get a bit tricky. That's where Excel ranking functions come into play.
The RANK() function is commonly used to determine the rank of a value within a dataset. It assigns a unique rank to each value based on its position in the dataset. But what if you have duplicate values? This is where the RANK.AVG() and RANK.EQ() functions come in handy. The former assigns an average rank to duplicate values, while the latter assigns a unique rank.
When it comes to calculating percentiles, Excel offers three functions: PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC(). The PERCENTILE() function calculates the k-th percentile of a dataset, while the INC version includes both endpoints in the calculation. On the other hand, the EXC version excludes both endpoints.
If you need to divide your dataset into quartiles, Excel provides two functions: QUARTILE() and QUARTILE.INC(). These functions calculate quartiles based on inclusive endpoints. However, if you prefer exclusive endpoints for your quartile calculations, you can use QUARTILE.EXC().
By familiarizing yourself with these Excel ranking functions - RANK(), RANK.AVG(), RANK.EQ(), PERCENTILE(), PERCENTILE.INC(),
PERCENTILE.EXC(),
QUARTILES(),
QUARTILES.INC(),
and
QUARTILES.EXC() Most students are drawn to these types of articles and information, but they are unable to prepare for their exams, If you have been struggling with your exams and want assistance, students can hire test takers for online classes and get higher grades on their examinations by providing them with the best available resources, including quality academic services.
When it comes to calculating percentiles, Excel offers three functions: PERCENTILE(), PERCENTILE.INC(), and PERCENTILE.EXC(). The PERCENTILE() function calculates the k-th percentile of a dataset, while the INC version includes both endpoints in the calculation. On the other hand, the EXC version excludes both endpoints. Most students are drawn to these types of articles and information, but they are unable to prepare for their exams, If you have been struggling with your exams and want assistance, students can pay to do my exam for me and get higher grades on their examinations by providing them with the best available resources, including quality academic services.
ReplyDeleteExcel ranking functions such as RANK(), RANK.AVG(), RANK.EQ(), PERCENTILE(), PERCENTILE.INC(), PERCENTILE.EXC(), QUARTILE(), QUARTILE.INC, and QUARTILE.EXC can be powerful tools for analyzing and organizing data. These functions allow users to easily determine the relative position of a value within a dataset, making it simpler to identify top performers or outliers.
ReplyDeleteThe RANK() function, for example, assigns a rank to each value in a range based on its position. This can be especially useful when comparing sales figures or performance metrics. Similarly, the PERCENTILE() function calculates the value at a given percentile within a dataset, allowing users to understand the distribution of their data.
In Excel 2010, nonparametric test ranking functions such as RANK, EQ, and AVG can be incredibly useful when it comes to analyzing data and making informed decisions. These functions are particularly valuable for those who are preparing to take my online exam and need to efficiently organize and rank their study materials.
ReplyDeleteThis Finance Dissertation Topic UK aims to examine the impact of fintech on the banking industry, particularly focusing on the opportunities it presents and the challenges it poses. The study will involve an in-depth analysis of the various aspects affected by fintech, such as customer behavior, banking operations, regulatory frameworks, and the overall financial landscape.One of the most notable developments is the emergence of financial technology, commonly known as fintech. Fintech refers to the innovative application of technology in providing financial services, including online banking, mobile payments, peer-to-peer lending, and digital currencies.eeking assistance from assignment help experts can be highly beneficial for students facing academic challenges. These experts possess extensive knowledge and expertise in various subjects, allowing them to provide invaluable guidance and support throughout the assignment process.
ReplyDeleteIn the world of statistical analysis, Excel 2010 offers a range of powerful functions that aid in conducting nonparametric tests. Three such functions are RANK.(), RANK.EQ(), and RANK.AVG(). These functions play a crucial role in ranking data, which is essential for nonparametric tests like the Mann-Whitney U Test, Wilcoxon Signed-Rank Test, and Friedman Test.
ReplyDeleteWhen it comes to global assignment help, having a solid understanding of these ranking functions can greatly enhance your ability to analyze and interpret data accurately. By using these functions in Excel 2010, you can easily rank your dataset based on specific criteria or conditions.
The RANK() function assigns a rank to each value in a dataset, with ties receiving the same rank. On the other hand, RANK.EQ() provides an exclusive rank to each value while handling ties differently. Lastly, RANK.AVG() assigns an average rank to tied values.
These ranking functions are invaluable tools for researchers and statisticians who rely on nonparametric tests to analyze their data effectively. By harnessing the power of Excel 2010's capabilities, you can streamline your analysis process and make informed decisions based on robust statistical findings.
In conclusion, understanding how to utilize RANK(), RANK.EQ(), and RANK.AVG() in Excel 2010 is crucial for anyone involved in global assignment help or statistical analysis. These functions enable you to perform nonparametric tests accurately and efficiently while ensuring reliable results that contribute to sound decision-making processes.
In the world of statistical analysis, Excel 2010 offers a range of powerful functions that aid in conducting nonparametric tests. Three such functions are RANK.(), RANK.EQ(), and RANK.AVG(). These functions play a crucial role in ranking data, which is essential for nonparametric tests like the Mann-Whitney U Test, Wilcoxon Signed-Rank Test, and Friedman Test.https://www.vertexminds.com/
ReplyDeleteOur successful journey of standing up and offering our services and solutions from the platform of Vertex Minds has been possible through the right combination of years of professional experience coupled with the right education, industry exposure, and skill-set.
Understanding ranking functions like RANK(), RANK.EQ(), and RANK.AVG() is crucial for effective data analysis in Excel. While RANK() remains functional, the introduction of RANK.EQ() in Excel 2010 enhances ranking capabilities. RANK.AVG() further extends options, providing an average rank for identical values. This evolution simplifies data interpretation, allowing users to choose the ranking method that best aligns with their analytical needs, enhancing the versatility of Excel in handling ranked data.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThe Garage Equipment Association (GEA) in the UK and Europe prioritizes safety and regulatory compliance with the Machinery Directive. Adhering to the Machinery Directive ensures that GEA members meet stringent health and safety requirements for their equipment, contributing to a secure working environment. From lifts to diagnostic tools, the directive covers a wide array of machinery, guaranteeing that each piece meets the necessary safety criteria. GEA's commitment to the Machinery Directive reflects its dedication to fostering a safe and reliable automotive service sector throughout the UK and Europe, enhancing the industry's overall safety standards and compliance.
ReplyDeletethank you for the helpful post, you can also hire best game developers for teen patti game development and poker game development company
ReplyDeleteIn Excel, the RANK function is used to assign a rank to a specific number within a list or range of values. The function calculates the relative position of a number compared to others in the dataset, indicating its rank. The RANK function is useful for analyzing data and determining the position of values in ascending or descending order.
ReplyDeletehearsay in court
dui lawyer fairfax va
tax and estate lawyer
henrico traffic lawyer
Tachographs play a crucial role in monitoring and recording commercial vehicle activities, ensuring compliance with regulations. If GEA has introduced a Digital Tachograph, it likely incorporates advanced features, improved efficiency, and enhanced capabilities to meet the evolving needs of the transportation industry while prioritizing legal compliance and safety standards.
ReplyDeleteEngage Experts revolutionizes budgeting and forecasting in accounting for businesses in the United Arab Emirates (UAE). This specialized platform seamlessly integrates advanced accounting practices with cutting-edge technology to optimize financial planning processes. Engage Experts employs robust accounting methodologies, incorporating precise data analysis and leveraging historical financial information specific to the UAE market.
ReplyDeleteNavigating through the maze of law assignments? Consider the convenience and expertise of Online Law Assignment Help. It's not just a service; it's your academic ally, ensuring clarity and excellence in every task.
ReplyDeleteA Thesis Statement Generator is a digital tool designed to help students and writers craft a clear, concise thesis statement for their essays or research papers. By inputting key information about their topic, arguments, and stance, the generator provides a well-structured thesis statement, streamlining the writing process and ensuring a strong foundation for their work.
ReplyDeleteEmbark on a visual journey with NOS Digital's Logo Designing in Dubai, UAE. Infused with innovation and cultural finesse, our designs transcend mere symbols, becoming potent expressions of brand identity. In the heart of Dubai's thriving landscape, NOS Digital captures the essence of your business, creating logos that resonate globally. Our meticulous approach blends creativity with strategic intent, ensuring your logo stands as a powerful emblem of distinction. Trust NOS Digital to elevate your brand presence, delivering bespoke logo designs that captivate audiences and carve a unique niche in the vibrant marketplace of Dubai, the epicenter of innovation and sophistication.
ReplyDeleteUnlock immersive storytelling with our professional Professional 3D animation services. Elevate your brand's visual narrative with stunning visuals and captivating motion. Let's bring your ideas to life in the third dimension.
ReplyDeleteYour piece deeply resonates with me! Your grasp of human dynamics is truly impressive. In a world inundated with shallow content, your authenticity stands out. You possess a rare talent for tapping into the complexities of human emotion and connection. Keep exploring these nuances; they provide valuable insights into the human experience. I'm excited to delve deeper into your thought-provoking work.
ReplyDeleteGoogle, the digital giant, is a cornerstone of the online world, offering an expansive array of tools and services that have revolutionized how we navigate, communicate, and access information. From its humble beginnings as a search engine to its current status as a multifaceted tech powerhouse, google has become synonymous with innovation and convenience. It's not just a company; it's a global force that touches nearly every aspect of our digital lives, from email to navigation to entertainment. With its commitment to excellence and user satisfaction, Google continues to shape the future of the internet, making our online experiences richer, more efficient, and more interconnected.
ReplyDeleteGreat work on this blog post! Breaking down the topic into simple steps is a strong approach. Your clear explanations make the content easily understandable. The visual examples and practical tips are invaluable. Your engaging writing style keeps me coming back for more. Keep up the excellent work! Looking forward to your future insights and posts. Thank you for sharing your expertise with us!
ReplyDeleteIf you are coming from a country where English is not your first language to study in Australia, you will need to take one of the following exams: IELTS, TOEFL, PTE, or CAE. There are two most popular tests: IELTS and TOEFL.
ReplyDeleteClick here to get more information: Study Abroad Consultancy
This blog post deeply resonated with me. Your ability to convey the significance of finding joy in the ordinary is remarkable. In our fast-paced world, we often neglect the little pleasures that enrich our lives. Your writing acts as a beacon, guiding us back to appreciating the small wonders around us. Thank you for sharing such heartfelt sentiments. Your words have a way of inspiring introspection and fostering a deeper appreciation for life's subtleties.
ReplyDeleteWow, this post is like a breath of fresh air! The way you break down complex ideas into easily digestible nuggets is truly impressive. I particularly loved how you intertwined real-life examples with practical advice. It's not just informative, it's engaging! Can't wait to implement these strategies in my own life. Keep up the fantastic work, and looking forward to your next enlightening post.
ReplyDeleteNavigating the demands of a BSN program requires effective time BSN Writing Services management and BSN Writing Services prioritization. BSN writing services help students optimize their time by handling complex writing tasks such as research papers, case studies, and capstone projects. By delegating these responsibilities to experienced writers, students can focus more effectively on their clinical practice, coursework, and personal commitments without compromising the quality of their academic work
ReplyDeleteWelcome to Camotions – your one-stop destination for premier maternity, baby/toddler/newborn, portrait and pre-wedding Photography services.
ReplyDeleteShashank Priyadarshi- a Postgraduate from NIT Jamshedpur, relinquished his easy 9-to-5 job just to pursue his passion for photography. He offers Kids photography in Gurgaon, newborn baby photography in Gurgaon His immaculate experience and seasoned approach in this field integrated with his his sense of creativity makes him toddler photography gurgaon stand as one of the best maternity photographer in Gurgaon. We also offer pre-wedding photography in Gurgaon
随着互联网的发展，留学生可以通过网络上各种评价平台、学术论坛以及社交媒体，获取其他学生对代写机构的评价和反馈。一个口碑良好的代写机构通常在服务质量、按时交付、客户沟通以及售后服务等方面表现出色，这种机构更值得信赖。留学生在选择代写服务时，可以参考其他学生的真实评价和经验，从中获得对代写机构更为客观的了解。同时，留学生还可以通过一些第三方评价网站，查看代写http://www.emwchinese.com/store机构的综合评分和用户的详细评论，从而做出更加明智的选择。如果一个代写机构的负面评价过多，或者存在一些不良记录，学生应当慎重考虑其服务的可靠性。
ReplyDelete