 (Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
This is one of the following eleven articles on creating user-interactive graphs of statistical distributions in Excel
Interactive Statistical Distribution Graph in Excel 2010 and Excel 2013
Interactive Graph of the Normal Distribution in Excel 2010 and Excel 2013
Interactive Graph of the Chi-Square Distribution in Excel 2010 and Excel 2013
Interactive Graph of the t-Distribution in Excel 2010 and Excel 2013
Interactive Graph of the t-Distribution’s PDF in Excel 2010 and Excel 2013
Interactive Graph of the t-Distribution’s CDF in Excel 2010 and Excel 2013
Interactive Graph of the Binomial Distribution in Excel 2010 and Excel 2013
Interactive Graph of the Exponential Distribution in Excel 2010 and Excel 2013
Interactive Graph of the Beta Distribution in Excel 2010 and Excel 2013
Interactive Graph of the Gamma Distribution in Excel 2010 and Excel 2013
Interactive Graph of the Poisson Distribution in Excel 2010 and Excel 2013
Overview of the Chi-
Square Distribution
The Chi-Square distribution is a family of continuous probability distributions. This is evidenced by the smooth shape of the above graph of a Chi-Square distribution’s PDF (Probability Density Function) curve. The Chi-Square distribution’s PDF curve is skewed to the right (has a disproportionately long tail on the right side) as shown in the above graph.
The Chi-Square distribution with k degrees of freedom is the distribution of the sum of squares of k random independent variables. Each variable is distributed according to the standard normal distribution, i.e., the variable is normally distributed with a mean that equals 0 and a standard deviation that equals 1.
The Chi-Square distribution is important because the distribution of a number of test statistics can be approximated by the Chi-Square distribution when specific conditions can be met.
The Chi-Square distribution is used in in hypothesis tests to determine whether distributions of categorical variables (the counts of variables in categories) are significantly different form each other. Two common hypothesis tests that use the Chi-Square distribution to approximate the test statistic’s distribution are the Chi-Square Independence Test and the Chi-Square Goodness-of-Fit Test.
The Chi-Square Goodness-of Fit Test compares the expected and observed frequencies of data in one-way tables. The Chi-Square Independence Test compares the expected and observed frequencies of data in two-way tables known as contingency tables. There are numerous other tests that are based upon the Chi-Square distribution as well.
Graphing the Chi-Square
Distribution’s PDF – Probability
Density Function
Step 1 – Create a Count
The Count becomes the basis for the X and Y values of each data point on the graph. This count will contain 100 points that count to 10 in increments of 0.1. The first number in the Count is 0.001 instead of 0 because The Excel formula CHISQ.DIST() does not calculate a value at X = 0. There are many ways to create a count. This count uses the method ROW() – ROW($B)/10 to increment each cell value in the column by 0.1.
 (Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
Step 2 – Create the X Values
One X value is created for each increment of the Count. The Chi-Square distribution’s only parameter, df – the degrees of freedom, determines how wide the graph will be and therefore are part of the X value calculation.
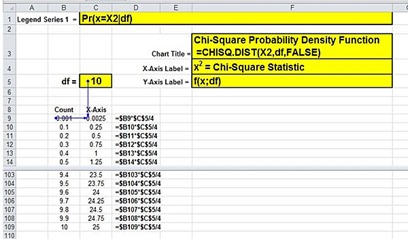
Step 3 – Create the Y Values
One Y value is created for each increment of the Count. The Y value of each data point is its PDF value. The Chi-Square’s PDF value requires the X value and its df as follows:

The following Excel-generated graph shows the Chi-Square’s PDF (Probability Density Function) for 10 degrees of freedom as the X value (the Chi-Square Statistic – Χ2) goes from 0 to 25.
The PDF value of a statistical distribution (the Y value) at a specific X value equals the probability that the value of a random sample will be equal to that X value if the population of data values from which the sample was taken is distributed according the stated distribution. The CDF value of a statistical distribution (the Y value) at a specific X value equals the probability that the value of a random sample will be up to that X value.

The process of creating an Excel area chart and connecting the user inputs to the chart is shown in detail in the section of this manual that provides instructions on how to create an interactive normal distribution PDF curve with outer tails.
The following Excel-generated graph shows the Chi-Square’s PDF (Probability Density Function) for 2 degrees of freedom as the X value (the Chi-Square Statistic – Χ2) goes from 0 to 25.
 (Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
The following Excel-generated graph shows the Chi-Square’s PDF (Probability Density Function) for 20 degrees of freedom as the X value (the Chi-Square Statistic – Χ2) goes from 0 to 25.
Note that the graph of the Chi-Square’s PDF resembles a wave rolling from left to right across the grid as the degrees of freedom are increased.
 (Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
Graphing the Chi-Square’s CDF –
Cumulative Distribution Function
The following Excel-generated graph shows the Chi-Square’s CDF (Cumulative Distribution Function) for 10 degrees of freedom as the X value (the Chi-Square Statistic – Χ2) goes from 0 to 25.
The CDF value of a statistical distribution (the Y value) at a specific X value equals the probability that the value of a random sample will be up to that X value if the population of data values from which the sample was taken is distributed according the stated distribution. The PDF value of a statistical distribution (the Y value) at a specific X value equals the probability that the value of a random sample will be equal to that X value.
The CDF of a statistical distribution always exists in the interval from 0 to 1.
 (Click On Image To See a Larger Version)
(Click On Image To See a Larger Version)
Excel Master Series Blog Directory
Click Here To See a List Of All
Statistical Topics And Articles In
This Blog
You Will Become an Excel Statistical Master!






I have been looking for a lot of time the way to understand how to do it correctly. Thank you very much for your extensive explanation. Also I would like to recommend a useful website with lots of different templates and charts http://charts.poweredtemplate.com/powerpoint-diagrams-charts/ppt-graph-charts/0/index.html
ReplyDeleteNANUM 명품 그래프게임 그래프사이트 부스타빗소셜그래프 추천 가장 완벽하게 그래프사이트를 운영하는 곳을 추천합니다 소셜그래프게임에 대한 안전성을 확실히 해결한 그래프사이트입니다 부스타빗을 조작 없이 즐길 수 있는 메이저사이트로 초대합니다 여기를 클릭하십시오 그래프게임
ReplyDeletevery nice blog post
ReplyDelete