Tuesday, November 23, 2010

Hypothesis Test In Excel To Find Out If Your Delivery Time Is Worsening

Using the Hypothesis

Test in Excel To Find

Out If Delivery Times

Have Gotten Worse




This article will explain how to use Excel to perform a Hypothesis Test to analyze delivery time for a business (a furniture store) has gotten worse. Specifically, we will show how to use Excel to perform One-Tailed, One-Sample, Unpaired Hypothesis Test of Mean to determine whether a furniture company's delivery time really has gotten worse.

This Hypothesis Test will be testing the Null Hypothesis that delivery time has not changed.

The advantages of statistical analysis in Excel to solve business statistics problems is that most problems can be solved in just one or two steps and there is no more need to look anything up on Normal Distribution tables.

Here is the problem:



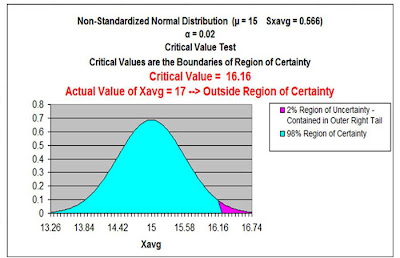
Problem: A furniture company states that its average delivery time is 15 days with a (population) standard deviation of 4 days. A random sample of 50 deliveries showed an average delivery time of 17 days. Determine within 98% certainty (0.02 significance level) whether delivery time has increased.

Here is the Before and After data for the delivery times:

"Before Data"

µ = "Before Data" mean = 15
σ = "Before Data" population standard deviation = 4


"After Data"

xavg = "After Data" sample average = 17
n = "After Data" Sample size = 50

α = Level of Significance = 0.02
Therefore there is 2% Max chance of error.
Therefore there is a 98% Level of Certainty Required.

Before we begin solving this problem, we need to know whether we are dealing with normally distributed data. If the data is not normally distributed, we have to use nonparametric statistical tests to solve this problem.

 Always Test for Normality First

Normality tests should be performed on the before and after delivery time data. Both data sets must be normally distributed to perform the well-known hypothesis test that is based upon the underlying data being normally distributed. This blog has numerous articles about how to perform normality testing and nonparametric testing if the data is not normally distributed.


The MOST Important Step

Determine What Type of Hypothesis

Test You Will Perform


1) Hypothesis Test of Mean or Proportion?

We know that this is a test of mean and not proportion because each individual sample taken can have a wide range of values: Any delivery time sample measurement from 12 to 18 days is probably reasonable.


2) One or Two-Tailed Hypothesis Test?

We know that this is a one-tailed test because we are trying to determine if the "After Data" mean delivery time is larger (worse) than the "Before Data" mean delivery time, not whether the mean mean delivery time is merely different, which would be a two-tailed test.


3) One or Two-Sample Hypothesis Test?

We know that only one sample needs to be taken because the population data being tested is already available.


4) Paired or Unpaired Hypothesis Test?

This is unpaired data because groups are sampled independently.

In this case, we are performing a One-Tailed, One-Sample, Unpaired Hypothesis Test of Mean to determine whether a furniture store's mean delivery time has really gotten worse. We will do this test in Excel. It is extremely important to establish the type of Hypothesis test. Each type of Hypothesis test uses a slightly (or very) different methodology and set of formulas.



The Four-Step Method That Solves ALL Hypothesis Tests


This problem can be solved using the standard four-step method for Hypothesis testing.


Step 1 - Create the Null and Alternate Hypotheses


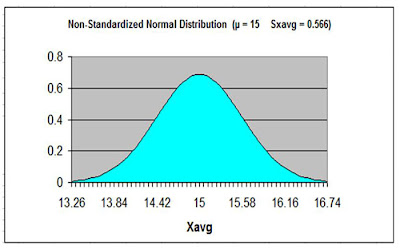
The Null Hypothesis normally states that both means are the same.If the "Before Data" population mean, µ, equals the "After Data" sample mean, xavg, then xavg = µ = 15

The Null Hypothesis states that both Before and After mean delivery times are the same, which is equivalent to:
The Null Hypothesis, which states that xavg is the same as µ (which is 15), is as follows:
Null Hypothesis, H0, is:    xavg = 15

*********************************

The Alternate Hypothesis states that the After Data mean delivery time is larger, which is equivalent to:

The Alternate Hypothesis, which states that xavg is larger than µ (which is 15), is as follows::

Alternate Hypothesis, H1 is:  xavg is greater than 15

*********************************


For this one-tailed test, the Alternative Hypothesis states that the value of the distributed variable xavg is larger than the value of 15 stated in the Null Hypothesis,

The Region of Uncertainty will be entirely in the right outer tail.

Note - the Alternative Hypothesis determines whether the Hypothesis test is a one-tailed test or a two-tailed test as follows:

One-tailed test -  (Value of variable) is greater than OR is less than (Constant)

Two-tailed test -  (Value of variable) does not equal (Constant)




Step 2 - Map the Normal Curve

We now create a Normal curve showing a distribution of the same variable that is used by the Null Hypothesis, which is xavg.

The mean of this Normal curve will occur at the same value of the distributed variable as stated in the Null Hypothesis.

Since the Null Hypothesis states that xavg = 15, the Normal curve will map the distribution of the variable xavg with a mean of xavg = 15.

************************************

This Normal curve will have a standard error that is calculated as the standard error of a sample taken from a population is normally calculated, as follows:

Sample Standard Error = sxavg = s / SQRT(n) = 4 / SQRT(50) = 0.566
Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse

Click On Image To See Larger Version





Step 3 - Map the Region of Certainty

The problem requires a 98% Level of Certainty so the Region of Certainty will contain 98% of the area under the Normal curve.

We know that this problem uses a one-tailed test with the Region of Uncertainty entirely contained in the outer right tail.

The Region of Uncertainty contains 2% of the total area under the Normal curve. The entire 98% Region of Certainty lies to the left of the 2% Region of Uncertainty, which is entirely contained in the outer right tail.

****************************************

We need to find out how far the boundary of the Region of Certainty is from the Normal curve mean. Calculating the number of standard errors from the Normal curve mean to the outer boundary of the Region of Certainty in the right tail for a one-tailed test is done as follows:

z98%,1-tailed = NORMSINV(1 - α) = NORMSINV(0.98) = 2.05

Excel Note - NORMSINV(x) = The number of standard errors from the Normal curve mean to a point right of the Normal curve mean at which x percent of the area under the Normal curve will be to the left of that point.

Additional note - For a one-tailed test, NORMSINV(x) can be used to calculate the number of standard errors from the Normal curve mean to the boundary of the Region of Certainty whether it is in the left or the right tail.

The Region of Certainty extends to the right of the Normal curve mean of xavg = 15 by 2.05 standard errors.

One standard error = sxavg = 0.566, so:

2.05 standard errors = (2.05) * (0.566) = 1.16

The outer boundary of the Region of Certainty has the value = µ + z95%,one-tailed * sxavg

which equals 15 + (2.05) * (0.566) = 15 + 1.16 = 16.16

Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse
Click Image To See Larger Version
The point, 16.16, is 2.05 standard errors from the Normal curve mean of xavg = 15

This point, 16.16, is the right boundary of the 98% Region of Certainty on the Normal curve.


Step 4 - Perform Critical Value and p-Value Tests

a) Critical Value Test

The Critical Value Test is the final test to determine whether to reject or not reject the Null Hypothesis. The p Value Test, described next, is an equivalent alternative to the Critical Value Test.

The Critical Value test tells whether the value of the actual variable, xavg, falls inside or outside of the Critical Value, which is the boundary between the Region of Certainty and the Region of Uncertainty.

If the actual value of the distributed variable, xavg, falls within the Region of Certainty, the Null Hypothesis is not rejected.

If the actual value of the distributed variable, xavg, falls outside of the Region of Certainty and, therefore, into the Region of Uncertainty, the Null Hypothesis is rejected and the Alternate Hypothesis is accepted.

The actual value of the variable xavg = 17 and is therefore to the right of (outside of) the outer right Critical Value (16.16), which is the boundary between the Regions of Certainty and Uncertainty in the right tail.

The actual value of the variable xavg is outside the Region of Certainty and therefore outside the Critical Value.

We therefore reject the Null Hypothesis and accept the Alternate Hypothesis which states that average delivery time has increased, with a maximum possible error of 2%.

Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse

Click On Image To See Larger Version


b) p Value Test

The p Value Test is an equivalent alternative to the Critical Value Test and also tells whether to reject or not reject the Null Hypothesis.

The p Value equals the percentage of area under the Normal curve that is in the tail outside of the actual value of the variable xavg.

For a one-tailed test, if the p Value is larger than α, the Null Hypothesis is not rejected.

For a two-tailed test, if the p Value is larger than α/2, the Null Hypothesis is not rejected.

For a one-tailed test, the Region of Uncertainty is contained entirely in one tail. Therefore the curve area contained by the Region of Uncertainty in that tail equals α.

For a two-tailed test, the Region of Uncertainty is split between both tails. Therefore the curve area contained by the Region of Uncertainty in that tail equals α/2.

The p Value for the actual value of the distributed variable, which in this case is greater than the mean (falls to the right of the mean in the right tail), is:

p Valuexavg = 1 - NORMSDIST( [ xavg - µ ] / sxavg )

Excel note - NORMSDIST(x) calculates the total area under the Normal curve to the LEFT of the point that is x standard errors to the right of the Normal curve mean. Since we are calculating the area to the RIGHT of this point, we use 1 - NORMSDIST..

p Valuexavg = 1 - NORMSDIST((17 - 15 ) / 0.566) = 1 - NORMSDIST(2.0/0.566) = 0.0002

The p Value (0.0002) is less than α (0.02), so the Null Hypothesis is rejected and the Alternate Hypothesis is accepted..

For a one-tailed test - When the p Value is less than α, the actual value of the distributed variable falls outside the Region of Certainty and the Null Hypothesis is rejected.

This is the case here.


Click Image To See Larger Version




*****************************************

Here is a link to this article if you wish to link to it:

Using the Hypothesis Test in Excel to Find Out If Your Delivery Time Has Gotten Worse


If You Like This, Then Share It...
Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse Hypothesis Test in Excel to Find Out If Your Delivery Time Got Worse


Hypothesis Test in Excel to Find Out If Your Advertising Worked

 




Excel Master Series Blog Directory

Statistical Topics and Articles In Each Topic

Posted by at
Labels: , , , , , , , ,

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)