Every Hypothesis Test
Done in Excel in 4 Steps
As an Internet marketing manager I use hypothesis testing all the time. There are quite a few great marketing uses of the hypothesis test with Excel that I will explain in detail in future articles of this blog. If you would like to see one very useful application of the hypothesis test in an article in this blog, check out this blog article on how to construct a split-tester in Excel that is better than the Google Website Optimizer. The basic test of this split-tester (and the Google Website Optimizer) is a hypothesis test.
Hypothesis Test Determines if Something Changed
In a nutshell, a hypothesis test is used to determine if something really has changed. For example, maybe you changed your Intenet marketing program slightly and you want to determine within 95% certainty whether the sales results that you've noticed are caused by your changes or are they just the result of random chance. The hypothesis test is the perfect tool to quickly answer that question. I will go so far as to say that the hypothesis test is my favorite Internet marketing statistical tool.Hypothesis Test - Solved With 4-Step Framework
Right now I would like to present a 4-step framework that can be used to solve ALL hypothesis tests. To my knowledge, I have not seen this framework presented anywhere else, but it definitely works for every type of hypothesis test.Hypothesis Test Must 1st Be Classified
Before you can begin the 4-step procedure, you must classify the hypothesis test you are about to perform. There are 4 separate categories in which the hypothesis test must be classified before applying the 4-step method. Each classification must be solved a slightly different way while applying the 4-step method. You therefore must determine upfront the type of hypothesis test so you will know exactly how to apply the 4-step method. The 4 categories of hypothesis tests are as follows:Problem Classification:
Select the proper choice of each of the four ways that a Hypothesis problem is classified as follows:
1) Mean Testing vs. Proportion Testing
• Proportion test samples have only two possible outcomes.• Mean test samples have multiple possible outcomes.
2) One-Tailed vs. Two-Tailed Testing
• Two-tailed tests determine whether two means are merely different.• One-tailed tests determine whether one mean is different in one
direction.
3) One-Sample vs. Two Sample Testing
• One sample is taken if original or "Before" comparison data isavailable.
• Two samples are taken if no comparison data is available.
4) Unpaired Data Testing vs. Paired Data Testing
• Paired data testing can be performed if "Before" and "After" dataare collected from the same objects. Mean testing can be
performed on paired data - Proportion testing cannot.
• Unpaired data testing is performed on data collected in groups.
Here below is a more detailed explanation of the above classifications:
1) Mean testing vs. Proportion testing -
This is the most important distinction that must be made. Mean testing and proportion are both solved using the same 4-step method but use different formulas.Mean testing – Hypothesis tests of mean use samples that can taken a range of values. For example, you are testing to determine if sales have gone up over the course of a month. The sampled daily sales can have a wide range of values.
Proportion testing – Hypothesis test of proportion use samples that can have only 2 values. For example, you are testing to determine whether new keywords in a Google AdWords ad group have increased conversion rate. You are sampling whether or not a click converted. Your sample has only 2 possible values. The click either converted or it didn’t.
2) One-tailed vs. Two-tailed testing
– This depends upon whether you are using the hypothesis test to determine whether the mean or proportion of one sampled group is merely different that the mean or proportion of another sampled group, or whether it is specifically different in one direction – whether it is larger or smaller.
One-tailed test – You are testing to determine if the mean or proportion of one sampled group is different in one specific direction than the mean or proportion of the other sampled group.
Two-tailed test – You only want to know if the mean or proportion of one group is different than that of the other group, but aren’t testing for direction.
– Whether you need to take one sample or two samples depends on whether you need have original or “before” sample data available. Two-sample testing is performed if no “before” data is available, or if no data is available on either side.
Paired data testing – An example of this would be “before” and “after” testing of the same object. For example, you are measuring whether sales really went up. Paired data testing can only be performed for a hypothesis test of mean, not proportion.
Unpaired data samples – Groups of unpaired data testing are treated independently of each other.
– Most hypothesis tests use unpaired data. Whether data is paired or unpaired depends on whether both samples were collected from the same objects or not.
The 4-Step Method To Solve ALL Hypothesis Tests
After having classified the hypothesis test according to the 4 categories, you are now ready to perform the 4-step method. In summary, the steps are as follows:
1) Create the Null and Alternate Hypotheses
2) Map the Normal Curve
- Showing the Distribution of the Variable Used by the Null Hypothesis.
3) Map the Region of Certainty
– The Area Under the Normal Curve That Corresponds With the Degree of Certainty You Require For Your Hypothesis Test.
4) Perform Either the Critical Value Test or the P Value Test
– to Determine Whether To Reject or Fail To Reject the Null Hypothesis
Without going into too much detail, we will take a brief look at solving a hypothesis test using the 4-step method.
Problem - One-Tailed, One-Sample, Unpaired Hypothesis Test of Mean
Testing whether a delivery time has gotten worse
Problem: A furniture company states that its average delivery time is 15 days with a (population) standard deviation of 4 days. A random sample of 50 deliveries showed an average delivery time of 17 days. Determine within 98% certainty (0.02 significance level) whether delivery time has increased.
SOLUTION:
We know that this is a test of mean and not proportion because each individual sample taken can have a wide range of values: Any delivery time sample measurement from 12 to 18 days is probably reasonable.
We know that this is a one-tailed test because we are trying to determine if the "After Data" mean delivery time is larger than the "Before Data" mean delivery time, not whether the mean delivery times are merely different.
We know that only one sample needs to be taken because the population data being tested is already available.
This is unpaired data because groups are sampled independently. Below is the Before and After sample data:
Step 1 - Create the Null and Alternate Hypotheses
The Null Hypothesis normally states that both means are the same.
If the "Before Data" population mean, µ, equals the "After Data" sample mean, xavg, then
xavg = µ = 15
The Null Hypothesis states that both means are the same, which is equivalent to:
The Null Hypothesis, which states that xavg is the same as µ (which is 15), is as follows:
Null Hypothesis, H0, is that xavg = 15
*****************************************************************************
The Alternate Hypothesis states that the After Data mean is larger, which is equivalent to:
The Alternate Hypothesis, which states that xavg is larger than µ (which is 15), is as follows:
Alternate Hypothesis, H1, is that xavg is greater than 15
Step 2 - Map the Normal Curve
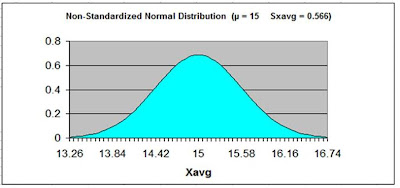
We now create a Normal curve showing a distribution of the same variable that is used by the Null Hypothesis, which is xavg.
The mean of this Normal curve will occur at the same value of the distributed variable as stated in the Null Hypothesis.
Since the Null Hypothesis states that xavg = 15, the Normal curve will map the distribution of the variable xavg with a mean of xavg = 15.
This Normal curve will have a standard error that is calculated as the standard error of a sample taken from a population is normally calculated, as follows:
Sample Standard Error = sxavg = σ / SQRT(n) = 4 / SQRT(50) = 0.566
Here is the Normal Curve mapped with the mean of xavg = 15
and Sample Standard Error = 0.566
Step 3 - Map the Region of Certainty
The problem requires a 98% Level of Certainty so the Region of Certainty will contain 98% of the area under the Normal curve.
We know that this problem uses a one-tailed test with the Region of Uncertainty entirely contained in the outer right tail. The Region of Uncertainty contains 2% of the total area under the Normal curve. The entire 98% Region of Certainty lies to the left of the 2% Region of Uncertainty, which is entirely contained in the outer right tail.
*****************************************************************************
We need to find out how far the boundary of the Region of Certainty is from the Normal curve mean. Calculating the number of standard errors from the Normal curve mean to the outer boundary of the Region of Certainty in the right tail for a one-tailed test is done in Excel as follows:
z 98%,1-tailed = NORMSINV(1 - α) = NORMSINV(0.98) = 2.05
Excel Note - NORMSINV(x) = The number of standard errors from the Normal curve mean to a point right of the Normal curve mean at which x percent of the area under the Normal curve will be to the left of that point.
Additional note - For a one-tailed test, NORMSINV(x) can be used to calculate the number of standard errors from the Normal curve mean to the boundary of the Region of Certainty whether it is in the left or the right tail.
The Region of Certainty extends to the right of the Normal curve mean of xavg = 15 by 2.05 standard errors.
One standard error = sxavg = 0.566, so:
2.05 standard errors = (2.05) * (0.566) = 1.16
The outer boundary of the Region of Certainty has the value = µ + z 98%,1-tailed * sxavg
which equals 15 + (2.05) * (0.566) = 15 + 1.16 = 16.16
The point, 16.16, is 2.05 standard errors from the Normal curve mean of xavg = 15
This point, 16.16, is the right boundary of the 98% Region of Certainty on the Normal curve.
Here is the mapping of the Region of Certainty:
Step 4 - Perform Critical Value and p-Value Tests
a) Critical Value Test
The Critical Value Test is the final test to determine whether to reject or not reject the Null Hypothesis. The p Value Test, described later, is an equivalent alternative to the Critical Value Test.
The Critical Value test tells whether the value of the actual variable, xavg, falls inside or outside of the Critical Value, which is the boundary between the Region of Certainty and the Region of Uncertainty.
If the actual value of the distributed variable, xavg, falls within the Region of Certainty, the Null Hypothesis is not rejected.
If the actual value of the distributed variable, xavg, falls outside of the Region of Certainty and, therefore, into the Region of Uncertainty, the Null Hypothesis is rejected and the Alternate Hypothesis is accepted.
In this case, the actual value of the variable, xavg = 17
The actual value of the variable xavg = 17 and is therefore to the right of (outside of) the outer right Critical Value (16.16), which is the boundary between the Regions of Certainty and Uncertainty in the right tail.
The actual value of the variable xavg is outside the Region of Certainty and therefore outside the Critical Value.
We therefore reject the Null Hypothesis and accept the Alternate Hypothesis which states that delivery time has increased, with a maximum possible error of 2%. This is shown in the following Excel graph:
b) p Value Test
The p Value Test is an equivalent alternative to the Critical Value Test and also tells whether to reject or not reject the Null Hypothesis.
The p Value equals the percentage of area under the Normal curve that is in the tail outside of the actual value of the variable xavg.
For a one-tailed test, if the p Value is larger than α, the Null Hypothesis is not rejected.
For a two-tailed test, if the p Value is larger than α/2, the Null Hypothesis is not rejected.
For a one-tailed test, the Region of Uncertainty is contained entirely in one tail. Therefore the curve area contained by the Region of Uncertainty in that tail equals α.
For a two-tailed test, the Region of Uncertainty is split between both tails. Therefore the curve area contained by the Region of Uncertainty in that tail equals α/2.
The p Value for the actual value of the distributed variable, which in this case is greater than the mean (falls to the right of the mean in the right tail), calculated in Excel is:
p Valuexavg = 1 - NORMSDIST( [ xavg - µ ] / sxavg )
Excel note - NORMSDIST(x) calculates the total area under the Normal curve to the left of the point that is x standard errors to the right of the Normal curve mean.
p Valuexavg = 1 - NORMSDIST((17 - 15 ) / 0.566)
= 1 - NORMSDIST(2/0.566)
= 0.0002
The p Value (0.0002) is less than α (0.02), so the Null Hypothesis is rejected and the Alternate Hypothesis is accepted..
For a one-tailed test---> When the p Value is less than α, the actual value of the distributed variable falls outside the Region of Certainty and the Null Hypothesis is rejected.
This is the case here as shown in the Excel graph:
In subsequent articles to this blog, I will show some very useful ways of using various types of hypothesis tests in Excel to improve your marketing. If you are interested in getting a deeper understanding of how to use Excel to perform hypothesis tests, Chapters 8 and 9 of the
Excel Statistical Master go into a lot of detail with many examples of doing every type of hypothesis test in Excel.
Feel free to comment on this blog article. Your opinion is very important.
Excel Master Series Blog Directory
Statistical Topics and Articles In Each Topic
- Histograms in Excel
- Bar Chart in Excel
- Combinations & Permutations in Excel
- Normal Distribution in Excel
- Overview of the Normal Distribution
- Normal Distribution’s PDF (Probability Density Function) in Excel 2010 and Excel 2013
- Normal Distribution’s CDF (Cumulative Distribution Function) in Excel 2010 and Excel 2013
- Solving Normal Distribution Problems in Excel 2010 and Excel 2013
- Overview of the Standard Normal Distribution in Excel 2010 and Excel 2013
- An Important Difference Between the t and Normal Distribution Graphs
- The Empirical Rule and Chebyshev’s Theorem in Excel – Calculating How Much Data Is a Certain Distance From the Mean
- Demonstrating the Central Limit Theorem In Excel 2010 and Excel 2013 In An Easy-To-Understand Way
- t-Distribution in Excel
- Binomial Distribution in Excel
- z-Tests in Excel
- t-Tests in Excel
- Overview of t-Tests: Hypothesis Tests that Use the t-Distribution
- 1-Sample t-Tests in Excel
- Overview of the 1-Sample t-Test in Excel 2010 and Excel 2013
- Excel Normality Testing For the 1-Sample t-Test in Excel 2010 and Excel 2013
- 1-Sample t-Test – Effect Size in Excel 2010 and Excel 2013
- 1-Sample t-Test Power With G*Power Utility
- Wilcoxon Signed-Rank Test As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
- Sign Test As a 1-Sample t-Test Alternative in Excel 2010 and Excel 2013
- 2-Independent-Sample Pooled t-Tests in Excel
- Overview of 2-Independent-Sample Pooled t-Test in Excel 2010 and Excel 2013
- Excel Variance Tests: Levene’s, Brown-Forsythe, and F Test For 2-Sample Pooled t-Test in Excel 2010 and Excel 2013
- Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro Wilk Tests For Two-Sample Pooled t-Test
- Two-Independent-Sample Pooled t-Test - All Excel Calculations
- 2-Sample Pooled t-Test – Effect Size in Excel 2010 and Excel 2013
- 2-Sample Pooled t-Test Power With G*Power Utility
- Mann-Whitney U Test in Excel as 2-Sample Pooled t-Test Nonparametric Alternative in Excel 2010 and Excel 2013
- 2-Sample Pooled t-Test = Single-Factor ANOVA With 2 Sample Groups
- 2-Independent-Sample Unpooled t-Tests in Excel
- 2-Independent-Sample Unpooled t-Test in Excel 2010 and Excel 2013
- Variance Tests: Levene’s Test, Brown-Forsythe Test, and F-Test in Excel For 2-Sample Unpooled t-Test
- Excel Normality Tests Kolmogorov-Smirnov, Anderson-Darling, and Shapiro-Wilk For 2-Sample Unpooled t-Test
- 2-Sample Unpooled t-Test Excel Calculations, Formulas, and Tools
- Effect Size for a 2-Independent-Sample Unpooled t-Test in Excel 2010 and Excel 2013
- Test Power of a 2-Independent Sample Unpooled t-Test With G-Power Utility
- Paired (2-Sample Dependent) t-Tests in Excel
- Paired t-Test in Excel 2010 and Excel 2013
- Excel Normality Testing of Paired t-Test Data
- Paired t-Test Excel Calculations, Formulas, and Tools
- Paired t-Test – Effect Size in Excel 2010, and Excel 2013
- Paired t-Test – Test Power With G-Power Utility
- Wilcoxon Signed-Rank Test As a Paired t-Test Alternative
- Sign Test in Excel As A Paired t-Test Alternative
- Hypothesis Tests of Proportion in Excel
- Hypothesis Tests of Proportion Overview (Hypothesis Testing On Binomial Data)
- 1-Sample Hypothesis Test of Proportion in Excel 2010 and Excel 2013
- 2-Sample Pooled Hypothesis Test of Proportion in Excel 2010 and Excel 2013
- How To Build a Much More Useful Split-Tester in Excel Than Google's Website Optimizer
- Chi-Square Independence Tests in Excel
- Chi-Square Goodness-Of-Fit Tests in Excel
- F Tests in Excel
- Correlation in Excel
- Pearson Correlation in Excel
- Spearman Correlation in Excel
- Confidence Intervals in Excel
- Overview of z-Based Confidence Intervals of a Population Mean in Excel 2010 and Excel 2013
- t-Based Confidence Intervals of a Population Mean in Excel 2010 and Excel 2013
- Minimum Sample Size to Limit the Size of a Confidence interval of a Population Mean
- Confidence Interval of Population Proportion in Excel 2010 and Excel 2013
- Min Sample Size of Confidence Interval of Proportion in Excel 2010 and Excel 2013
- Simple Linear Regression in Excel
- Overview of Simple Linear Regression in Excel 2010 and Excel 2013
- Simple Linear Regression Example in Excel 2010 and Excel 2013
- Residual Evaluation For Simple Regression in Excel 2010 and Excel 2013
- Residual Normality Tests in Excel – Kolmogorov-Smirnov Test, Anderson-Darling Test, and Shapiro-Wilk Test For Simple Linear Regression
- Evaluation of Simple Regression Output For Excel 2010 and Excel 2013
- All Calculations Performed By the Simple Regression Data Analysis Tool in Excel 2010 and Excel 2013
- Prediction Interval of Simple Regression in Excel 2010 and Excel 2013
- Multiple Linear Regression in Excel
- Basics of Multiple Regression in Excel 2010 and Excel 2013
- Multiple Linear Regression Example in Excel 2010 and Excel 2013
- Multiple Linear Regression’s Required Residual Assumptions
- Normality Testing of Residuals in Excel 2010 and Excel 2013
- Evaluating the Excel Output of Multiple Regression
- Estimating the Prediction Interval of Multiple Regression in Excel
- Regression - How To Do Conjoint Analysis Using Dummy Variable Regression in Excel
- Logistic Regression in Excel
- Logistic Regression Overview
- Logistic Regression Performed in Excel 2010 and Excel 2013
- R Square For Logistic Regression Overview
- Excel R Square Tests: Nagelkerke, Cox and Snell, and Log-Linear Ratio in Excel 2010 and Excel 2013
- Likelihood Ratio Is Better Than Wald Statistic To Determine if the Variable Coefficients Are Significant For Excel 2010 and Excel 2013
- Excel Classification Table: Logistic Regression’s Percentage Correct of Predicted Results in Excel 2010 and Excel 2013
- Hosmer-Lemeshow Test in Excel – Logistic Regression Goodness-of-Fit Test in Excel 2010 and Excel 2013
- Single-Factor ANOVA in Excel
- Overview of Single-Factor ANOVA
- Single-Factor ANOVA Example in Excel 2010 and Excel 2013
- Shapiro-Wilk Normality Test in Excel For Each Single-Factor ANOVA Sample Group
- Kruskal-Wallis Test Alternative For Single Factor ANOVA in Excel 2010 and Excel 2013
- Levene’s and Brown-Forsythe Tests in Excel For Single-Factor ANOVA Sample Group Variance Comparison
- Single-Factor ANOVA - All Excel Calculations
- Overview of Post-Hoc Testing For Single-Factor ANOVA
- Tukey-Kramer Post-Hoc Test in Excel For Single-Factor ANOVA
- Games-Howell Post-Hoc Test in Excel For Single-Factor ANOVA
- Overview of Effect Size For Single-Factor ANOVA
- ANOVA Effect Size Calculation Eta Squared (?2) in Excel 2010 and Excel 2013
- ANOVA Effect Size Calculation Psi (?) – RMSSE – in Excel 2010 and Excel 2013
- ANOVA Effect Size Calculation Omega Squared (?2) in Excel 2010 and Excel 2013
- Power of Single-Factor ANOVA Test Using Free Utility G*Power
- Welch’s ANOVA Test in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
- Brown-Forsythe F-Test in Excel Substitute For Single-Factor ANOVA When Sample Variances Are Not Similar
- Two-Factor ANOVA With Replication in Excel
- Two-Factor ANOVA With Replication in Excel 2010 and Excel 2013
- Variance Tests: Levene’s and Brown-Forsythe For 2-Factor ANOVA in Excel 2010 and Excel 2013
- Shapiro-Wilk Normality Test in Excel For 2-Factor ANOVA With Replication
- 2-Factor ANOVA With Replication Effect Size in Excel 2010 and Excel 2013
- Excel Post Hoc Tukey’s HSD Test For 2-Factor ANOVA With Replication
- 2-Factor ANOVA With Replication – Test Power With G-Power Utility
- Scheirer-Ray-Hare Test Alternative For 2-Factor ANOVA With Replication
- Two-Factor ANOVA Without Replication in Excel
- Creating Interactive Graphs of Statistical Distributions in Excel
- Interactive Statistical Distribution Graph in Excel 2010 and Excel 2013
- Interactive Graph of the Normal Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Chi-Square Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the t-Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Binomial Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Exponential Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Beta Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Gamma Distribution in Excel 2010 and Excel 2013
- Interactive Graph of the Poisson Distribution in Excel 2010 and Excel 2013
- Solving Problems With Other Distributions in Excel
- Solving Uniform Distribution Problems in Excel 2010 and Excel 2013
- Solving Multinomial Distribution Problems in Excel 2010 and Excel 2013
- Solving Exponential Distribution Problems in Excel 2010 and Excel 2013
- Solving Beta Distribution Problems in Excel 2010 and Excel 2013
- Solving Gamma Distribution Problems in Excel 2010 and Excel 2013
- Solving Poisson Distribution Problems in Excel 2010 and Excel 2013
- Optimization With Excel Solver
- Maximizing Lead Generation With Excel Solver
- Minimizing Cutting Stock Waste With Excel Solver
- Optimal Investment Selection With Excel Solver
- Minimizing the Total Cost of Shipping From Multiple Points To Multiple Points With Excel Solver
- Knapsack Loading Problem in Excel Solver – Optimizing the Loading of a Limited Compartment
- Optimizing a Bond Portfolio With Excel Solver
- Travelling Salesman Problem in Excel Solver – Finding the Shortest Path To Reach All Customers
- Chi-Square Population Variance Test in Excel
- Analyzing Data With Pivot Tables
- SEO Functions in Excel
- Time Series Analysis in Excel










Mua vé máy bay tại Aivivu, tham khảo
ReplyDeleteVe may bay di My
vé máy bay về việt nam từ mỹ
vé máy bay khứ hồi từ đức về việt nam
chuyến bay nhật bản về việt nam
vé máy bay hàn quốc hà nội
vé máy bay giá rẻ từ Canada về Việt Nam
khách sạn cách ly tại hà nội
Chuyến bay cho chuyên gia nước ngoài
This framework for hypothesis tests seems very useful.
ReplyDelete